Cho hình lăng trụ ABC. A'B'C' có đáy ABC là tam giác vuông tại A. cạnh BC=2a và
B
'
B
C
^
nhọn. Biết (BCC'B') vuông góc với (ABC) và (ABB'A') tạo với (ABC) góc 450. Thể tích của khối lăng trụ ABC. A'B'C' bằng: A.
a
3
7
B.
3
a
3
7
C.
6
a
3
7
D.
a
3
3
7
...
Đọc tiếp
Cho hình lăng trụ ABC. A'B'C' có đáy ABC là tam giác vuông tại A. cạnh BC=2a và B ' B C ^ nhọn. Biết (BCC'B') vuông góc với (ABC) và (ABB'A') tạo với (ABC) góc 450. Thể tích của khối lăng trụ ABC. A'B'C' bằng:
A. a 3 7
B. 3 a 3 7
C. 6 a 3 7
D. a 3 3 7
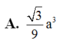
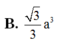
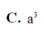
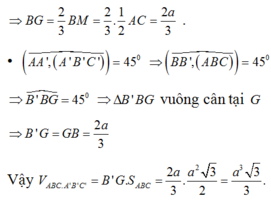
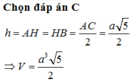
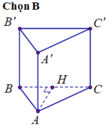
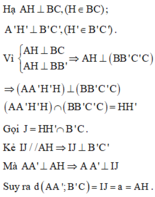
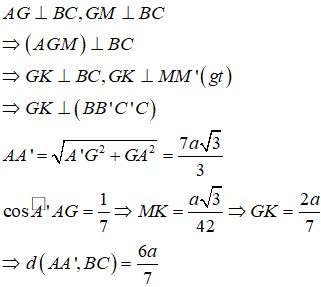
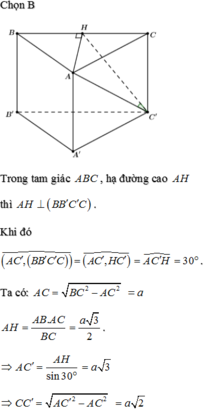
Chọn B
Do ABC là tam giác vuông tại A, cạnh BC=2a và A B C ^ = 60 0 nên AB=a, AC=√3
Gọi H là hình chiếu vuông góc của B' lên BC => H thuộc đoạn BC (do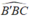
nhọn)
Kẻ HK song song AC (K thuộc AB)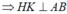
(do ABC là tam giác vuông tại A).
Ta có ΔBB'H vuông tại H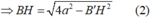
Mặt khác HK song song AC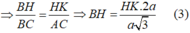
Từ (1), (2) và (3) suy ra: