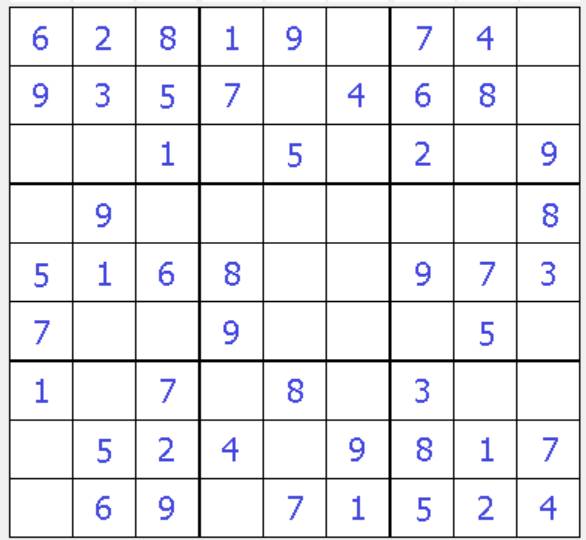
Sudoku là một loại trò chơi lôgic và cách chơi là điền số từ 1 đến 9 vào những ô trống sao cho mỗi cột dọc, mỗi hàng ngang, mỗi phân vùng nhỏ (ô 3x3) có đủ các số từ 1 đến 9 mà không được lặp lại. Có bao nhiêu bảng Sudoku có thể tạo ra?
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
CM
2 tháng 5 2019
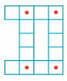
Tổng các số từ 1 đến 14 là : (14 + 1) x 14 : 2 = 105.
Tổng các số của 4 hàng là : 30 x 4 = 120.
Tổng bốn số ở bốn ô có dấu * là : 120 - 105 = 15.
Cặp bốn số ở bốn ô có dấu * là một trong các trường hợp sau:
15 = 1 + 2 + 3 + 9 (1)
= 1 + 2 + 4 + 8 (2)
= 1 + 2 + 5 + 7 (3)
= 1 + 3 + 4 + 7 (4)
= 1 + 3 + 5 + 7 (5)
= 2 + 3 + 4 + 6 (6)
Từ mỗi trường hợp này có thể tạo nên nhiều cách sắp xếp các số khác nhau.
29 tháng 12 2016
Bài 1/ Ta có
13n + 7 chia hết cho 5
=> 10n + 3n + 10 - 3 chia hết cho 5
=> 3n - 3 chia hết cho 5
=> 3(n - 1) chia hết cho 5
=> n - 1 chia hết cho 5
=> n - 1 = 5k
=> n = 5k + 1
Vậy với n = 5k + 1(k tự nhiên) thì 13n + 7 chia hết cho 5
NN
Nguyễn Ngọc Anh Minh
CTVHS
VIP
29 tháng 6 2020
Tổng của 9 số theo hàng là
480+570+660=1710
Tổng 9 số theo cột là
540+572+509=1621
Tổng 9 số theo hàng khác tổng 9 số theo cột nên không xảy ra trường hợp này
