Cho tam giác ABC có góc B = 60o , góc C = 40O tia phân giác của góc B cắt AC tại D, tia phân giác của C cắt AB tại BD và CK cắt nhau tại I. Tính góc DIK ?
giúp mình với
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
18 tháng 2 2023
a,Vì tam giác ABC đều => BD,CE vừa là tia phân giác vừa là đường cao=>BD vuông góc AC và CE vuông góc AB
b, vì hai tia phân giác BD và CE cắt nhau tại O suy ra O là tâm tam giác ABC suy ra OA = OB = OC (tính chất)
c, ta có góc AOB + góc BOC + góc COA = 360 độ mà AOB = BOC= COA Suy ra 3 AOB= 360 suy ra AOB = 120 vậy AOB=BOC=COA=120
CM
19 tháng 11 2018
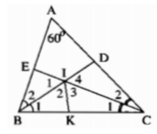
Trong ΔABC, ta có:
∠A +∠B +∠C = 180o (tổng ba góc trong tam giác)
⇒∠B +∠C = 180 - ∠A = 180 - 60 = 120o
+) Vì BD là tia phân giác của ABC nên: ∠(B1 ) = ∠(B2) = 1/2 ∠B
Vì CE là tia phân giác của góc ACB nên: ∠(C1 ) = ∠(C2) = 1/2 ∠ C
Do đó:
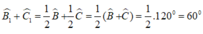
Trong ΔBIC, ta có:
∠(BIC) = 180o(∠(B1 ) + ∠(C1) = 180o - 60o = 120o
Kẻ tia phân giác ∠(BIC) cắt cạnh BC tại K
Suy ra: ∠(I2 ) = ∠(I3 ) = 1/2 ∠(BIC) = 60o
Ta có: ∠(I1 ) + ∠(BIC) = 180o (hai góc kề bù)
⇒ ∠(I1 ) = 180o-∠(BIC) = 180o - 120o = 60o
∠(I4 ) = ∠(I1) = 60o(vì hai góc đối đỉnh)
Xét ΔBIE và ΔBIK, ta có
∠(B2) = ∠(B1) (vì BD là tia phân giác của góc ABC)
BI cạnhchung
∠(I1) = ∠(I2) = 60o
Suy ra: ΔBIE = ΔBIK(g.c.g)
IK = IE (hai cạnh tương ứng) (1)
Xét ΔCIK và ΔCID, ta có
∠(C1) = ∠(C2) ( vì CE là tia phân giác của góc ACB).
CI cạnh chung
∠(I3) = ∠(I4) = 60o
Suy ra: ΔCIK = ΔCID(g.c.g)
IK = ID (hai cạnh tương ứng) (2)
Từ (1) và (2) suy ra: IE = ID
NH
3 tháng 12 2016
tam giác ABC có góc B=góc C
=> tam giác ABC cân tại A
=> AB=AC
Ma goc ACE = 1/2 ACB
góc ABD = 1/2 ABC (Vì CE và BD là tia phân giác của góc ACB và ABC)
ma ACB=ABC
=> ACE=ABD
Xét tam giác ABD và tam giác ACE
Có AB=AC(chứng minh trên)
goc A chung
ABD=ACE (chứng minh trên)
=> BD=CE (2 góc tương ứng)
19 tháng 1 2022
mình là màu xanh cho đồng cỏ còn bạn là màu đỏ trong tim mình >_<
7 tháng 1 2022
Xét t/g ABC có
=> t/g ABC cân tại A.
=> AB = AC (t/c).
Có
=>
=> (do BD, CE là pg góc B và C)
Xét t/g ABD và t/g ACE có
:chung
AB = AC (cmt)
=> t/g ABD = t/g ACE (g.c.g)
=> BD = CE (2 cạnh t/ứ).
9 tháng 12 2021
Kẻ phân giác IH của \(\widehat{BIC}\)
Ta có \(\widehat{ABC}+\widehat{ACB}=180^0-\widehat{BAC}=120^0\)
Mà BI,CI là phân giác \(\widehat{ABC};\widehat{ACB}\Rightarrow\widehat{IBC}+\widehat{ICB}=\dfrac{1}{2}\left(\widehat{ABC}+\widehat{ACB}\right)=60^0\)
Xét tam giác IBC: \(\widehat{BIC}=180^0-\left(\widehat{IBC}+\widehat{ICB}\right)=120^0\)
\(\Rightarrow\widehat{BIH}=\widehat{CIH}=\dfrac{1}{2}\widehat{BIC}=60^0\)
Lại có \(\widehat{BIE}=\widehat{DIC}=180^0-\widehat{BIC}=60^0\) (kề bù)
Do đó \(\widehat{BIH}=\widehat{CIH}=\widehat{BIE}=\widehat{DIC}\)
\(\left\{{}\begin{matrix}\widehat{BIH}=\widehat{BIE}\\BI\text{ chung}\\\widehat{IBE}=\widehat{IBH}\end{matrix}\right.\Rightarrow\Delta BEI=\Delta BHI\left(g.c.g\right)\\ \Rightarrow EI=HI\left(1\right)\\ \left\{{}\begin{matrix}\widehat{CIH}=\widehat{DIC}\\CI\text{ chung}\\\widehat{HIC}=\widehat{DIC}\end{matrix}\right.\Rightarrow\Delta CDI=\Delta CHI\left(g.c.g\right)\\ \Rightarrow DI=HI\left(2\right)\\ \left(1\right)\left(2\right)\Rightarrow IE=ID\)
