Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
b: PTHĐGĐ là:
1/2x^2-x-4=0
=>x^2-2x-8=0
=>(x-4)(x+2)=0
=>x=4 hoặc x=-2
=>y=8 hoặc y=2
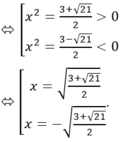
a: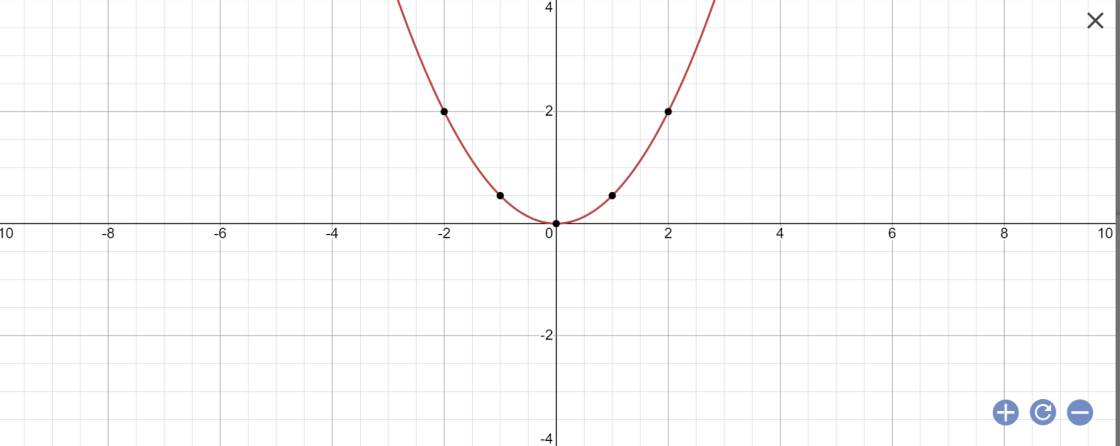 
b: Tọa độ giao điểm là:
\(\left\{{}\begin{matrix}\dfrac{1}{2}x^2-x-4=0\\y=x+4\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}x^2-2x-8=0\\y=x+4\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}\left(x-4\right)\left(x+2\right)=0\\y=x+4\end{matrix}\right.\Leftrightarrow\left(x,y\right)\in\left\{\left(4;8\right);\left(-2;2\right)\right\}\)
Đáp án A.
Phương trình hoành độ giao điểm:
x4 – 4x2 – 2 = 1 – x2 ⇔ x4 – 3x2 – 3 = 0
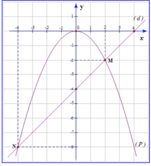
1) Vẽ hai đồ thị ( P ) và ( d ) trên cùng một mặt phẳng tọa độ.
* y = − 1 2 x 2 Hàm số xác định với mọi x ∈ ℝ Bảng giá trị
Nhận xét: Đồ thị hs là một parabol đi qua gốc tọa độ,nhận trục tung làm trục đối xứng nằm phía dưới trục hoành,O là điểm cao nhất *y=x-4 Đồ thị hs là đường thẳng đi qua hai điểm (0;-4) và (4;0) |
|
2)Hoành độ giao điểm của (P) và (d) là nghiệm của phương trình
−
1
2
x
2
=
x
−
4
⇔
x
2
−
2
x
−
8
=
0
Δ ' = 1 + 8 = 9 > 0 nên phương trình có 2 nghiệm phân biệt x1=2;x2=-4
x1=2 => y1=-2 ; x2=-4 => y2=-8
Vậy tọa độ giao điểm của (P) và (d) là (2;-2) và (-4;-8)
a: Thay x=1 và y=0 vào (d), ta được:
1-2m+3=0
\(\Leftrightarrow m=2\)
Đáp án A
Phương pháp:
Đặt Đáp án A
Phương pháp:
Đặt f(x) = a(x – x1)(x – x2)(x – x3)(x – x4), tính đạo hàm của hàm số y = f(x)
Xét hàm số h x = f ' x f x và chứng minh f(x).f’’(x) – [f’(x)]2 < 0 ∀ x ∉ x 1 ; x 2 ; x 3 ; x 4
Cách giải: Đồ thị hàm sốy = f(x) cắt trục hoành tại bốn điểm phân biệt nên
f(x) = a(x – x1)(x – x2)(x – x3)(x – x4)
=> f ’(x) = a(x – x1)(x – x2)(x – x3)(x – x4) + a(x – x1)(x – x3)(x – x4) + a(x – x1)(x – x2)(x – x4) + a(x – x1)(x – x2)(x – x3)
f ’(x) = f(x) 1 x - x 1 + 1 x - x 2 + 1 x - x 3 + 1 x - x 4 ∀ x ∉ x 1 ; x 2 ; x 3 ; x 4 => f’(x) ≠ 0 ∀ x ∉ x 1 ; x 2 ; x 3 ; x 4
Đặt h x = f ' x f x = 1 x - x 1 + 1 x - x 2 + 1 x - x 3 + 1 x - x 4 ∀ x ∉ x 1 ; x 2 ; x 3 ; x 4
Ta có
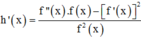
= - 1 ( x - x 1 ) 2 + - 1 ( x - x 2 ) 2 + - 1 ( x - x 3 ) 2 + - 1 ( x - x 4 ) 2 <0 ∀ x ∉ x 1 ; x 2 ; x 3 ; x 4
=> f ''(x).f(x) – [f’(x)]2 < 0 ∀ x ∉ x 1 ; x 2 ; x 3 ; x 4
=> g(x) = [f’(x)]2 – f(x).f’’(x)>0 ∀ x ∉ x 1 ; x 2 ; x 3 ; x 4
Khi f(x) = 0 => f '(x) ≠ 0 => g(x) = [f’(x)]2 – f(x).f’’(x) ≠ 0
Vậy đồ thị hàm số y = g(x) = [f’(x)]2 – f(x).f’’(x) không cắt trục Ox
