Có bao nhiêu giá trị nguyên thuộc khoảng (-9; 9) của tham số m để bất phương trình 3 log x ≤ 2 log m x − x 2 − 1 − x 1 − x
có nghiệm thực?
A. 6
B. 7
C. 10
D. 11
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Ta có yêu cầu bài toán tương đương với:

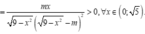
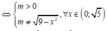
![]()
![]()
Vậy có tất cả 7 số nguyên thoả mãn.
Chọn đáp án B.

Chọn đáp án B.
Ta có yêu cầu bài toán tương đương với
y ' = m x 9 - x 2 ( 9 - x 2 - m ) 2 > 0 , ∀ x ∈ 0 ; 5
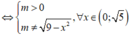
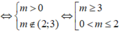
![]()
Vậy có tất cả 7 số nguyên thoả mãn.

Chọn A
Do ![]() với
với ![]() nên
nên
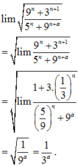
Theo đề bài ta có
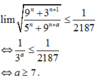
Do a là số nguyên thuộc khoảng (0;2018 nên có ![]() có 2011 giá trị của a.
có 2011 giá trị của a.

TH1 : Đồ thị hàm số y = 3mx2 - (m - 9)x + 8 - m2 có hai điểm phân biệt đối xứng nhau qua gốc tọa độ khi hàm số trên là hàm số lẻ trên tập xác định R
Khi đó f(x) + f(-x) = 0
⇒ 3mx2 + 3mx2 - (m - 9)x + 8- m2 + (m - 9)x - m2 + 8 = 0
⇒ 6mx2 + 16 = 0 (không có m)

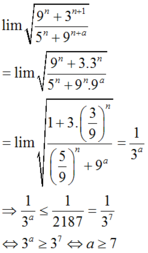
Kết hợp điều kiện đề bài
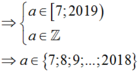
Vậy có 2018 - 7 + 1 = 2012 giá trị của a thỏa mãn.
Chọn C.
Đáp án B.
Phương pháp:
Bất phương trình m ≥ f x , x ∈ D có nghiệm khi và chỉ khi m ≥ M i n D f x .
Cách giải:
ĐKXĐ: 0 < x < 1
3 log x ≤ 2 log m x − x 2 − 1 − x 1 − x ⇔ m x − x 2 − 1 − x 1 − x ≥ x x
⇔ m ≥ x x + 1 − x 1 − x x − x 2 , x ∈ 0 ; 1
Để bất phương trình đã cho có nghiệm thực thì m ≥ M i n 0 ; 1 f x , f x = x x + 1 − x 1 − x x − x 2
Xét
f x = x x + 1 − x 1 − x x − x 2 = x + 1 − x 1 − x x − 1 x x − 1 , x ∈ 0 ; 1
Đặt t = x + 1 − x , t ∈ 1 ; 2
Khi đó,
f x = x + 1 − x 1 − x 1 − x x 1 − x = t 1 − t 2 − 1 2 t 2 − 1 2 = t 3 − t 2 t 2 − 1 = 3 t − t 3 t 2 − 1 = g t
g ' t = − t 4 − 3 t 2 − 1 2 < 0 , ∀ t ∈ 1 ; 2
⇒ g t min = g 2 = 3 2 − 2 2 2 − 1 = 2 ⇒ M i n 0 ; 1 f x = 2 ⇒ m ≥ 2
Mà
m ∈ − 9 ; 9 ⇒ m ∈ 2 ; 3 ; 4 ; ... ; 8 ⇒
Có 7 giá trị thỏa mãn.