Gọi I là tâm của đường tròn C : x - 1 2 + y - 1 2 = 4 . Số các giá trị nguyên của m để đường thẳng x+y-m=0 cắt đường tròn (C) tại hai điểm phân biệt A, B sao cho tam giác IAB có diện tích lớn nhất là
A.1
B.3
C.2
D.0
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Chọn C
![]() .
.
Vì ![]() nên phương trình
nên phương trình ![]() có 2 nghiệm phân biệt.
có 2 nghiệm phân biệt.
Do đó hàm số có hai điểm cực trị ![]() .
.
Giả sử hàm số có hai điểm cực trị lần lượt là ![]() và
và ![]() , với
, với ![]() ,
, ![]() là nghiệm của phương trình
là nghiệm của phương trình ![]() .
.
Thực hiện phép chia ![]() cho
cho ![]() ta được :
ta được : ![]() .
.
Khi đó ta có: 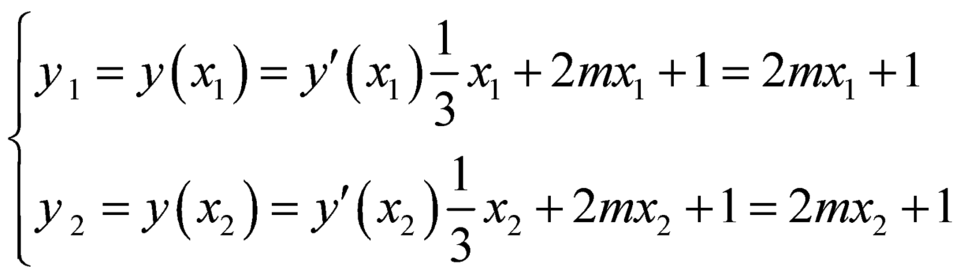 .
.
Ta thấy, toạ độ hai điểm ![]() và
và ![]() thoả mãn phương trình
thoả mãn phương trình ![]() .
.
Do đó, phương trình đường thẳng qua hai điểm cực trị là ![]() .
.
Ta thấy ![]() luôn qua
luôn qua ![]() .
.
Đặt ![]()
![]() .
.
![]() .
.
Xét hàm số ![]() ,
, ![]() .
.
![]() ,
, ![]() .
.
Suy ra hàm số ![]() liên tục và đồng biến trên
liên tục và đồng biến trên ![]() .
.
Do đó ![]() .
.
Vậy ![]() đạt giá trị lớn nhất
đạt giá trị lớn nhất ![]()
![]() .
.

Đạo hàm y’ = 3x2 – 3m
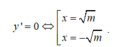
Hàm số có 2 cực trị khi và chỉ khi : m> 0
Khi đó tọa độ 2 điểm cực trị của đồ thị hàm số là:
M ( m ; - 2 m m + 2 ) N ( - m ; 2 m m + 2 ) ⇒ M N → = ( - 2 m ; 4 m m )
Phương trình đường thẳng MN: 2mx+ y-2=0
Ta có :
S ∆ I A B = 1 2 I A . I B . sin A I B ^ = 1 2 sin A I B ^ ≤ 1 2
Dấu bằng xảy ra khi
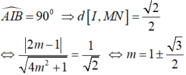
Chọn B.

Chọn B
[Phương pháp tự luận]
y ' = 3 x 2 - 3 m
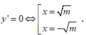
Hàm số có 2 cực trị khi và chỉ khi m > 0
Khi đó tọa độ 2 điểm cực trị của đồ thị hàm số là : M ( m ; - 2 m m + 2 )
![]()
Phương trình đt MN : 2 m x + y - 2 = 0
![]()
![]()
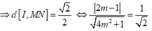
⇔ m = 1 ± 3 2