Cho a , b , c > 0 , a ≠ 1 ; b ≠ 1 . Trong các khẳng định sau, khẳng định nào sai?
A. log a b . c = log a b + log a c
B. log a b . log b c = log a c
C. log a b = 1 log b a
D. log a c b = c log a b
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

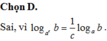

\(\frac{1}{a}+\frac{1}{a-b}=\frac{1}{b-c}-\frac{1}{c}\Leftrightarrow\frac{1}{a-b}+\frac{1}{c}=\frac{1}{b-c}-\frac{1}{a}\)
\(\Leftrightarrow\frac{c+a-b}{\left(a-b\right)c}=\frac{a-b+c}{\left(b-c\right)a}\)(1)
Do \(\frac{a}{c}=\frac{a-b}{b-c}\Leftrightarrow a\left(b-c\right)=\left(a-b\right)c\)nên (1) đúng, đẳng thức được CM

1. Ta có : \(\left(\frac{1}{a}-\frac{1}{b}\right)^2\ge0\Rightarrow\frac{1}{a^2}+\frac{1}{b^2}\ge\frac{2}{ab}\)
Tương tự : \(\frac{1}{b^2}+\frac{1}{c^2}\ge\frac{2}{bc}\); \(\frac{1}{a^2}+\frac{1}{c^2}\ge\frac{2}{ac}\)
\(\Rightarrow\frac{1}{a^2}+\frac{1}{b^2}+\frac{1}{c^2}\ge\frac{1}{ab}+\frac{1}{bc}+\frac{1}{ac}\). Dấu " = " xảy ra \(\Leftrightarrow\)a = b = c
\(\frac{1}{a}+\frac{1}{b}+\frac{1}{c}=3\Rightarrow\frac{1}{a^2}+\frac{1}{b^2}+\frac{1}{c^2}+2\left(\frac{1}{ab}+\frac{1}{bc}+\frac{1}{ac}\right)=9\)
\(9\le3\left(\frac{1}{a^2}+\frac{1}{b^2}+\frac{1}{c^2}\right)\)\(\Rightarrow\frac{1}{a^2}+\frac{1}{b^2}+\frac{1}{c^2}\ge3\)
Dấu " = " xảy ra \(\Leftrightarrow\)a = b = c = 1
\(\frac{1}{a}+\frac{1}{b}+\frac{1}{c}=7\)\(\Rightarrow\frac{1}{a^2}+\frac{1}{b^2}+\frac{1}{c^2}+2\left(\frac{1}{ab}+\frac{1}{bc}+\frac{1}{ac}\right)=49\)
\(\Rightarrow\frac{1}{a^2}+\frac{1}{b^2}+\frac{1}{c^2}+2.\frac{a+b+c}{abc}=49\)
\(\Rightarrow\frac{1}{a^2}+\frac{1}{b^2}+\frac{1}{c^2}=49\)

tuổi con HN là :
50 : ( 1 + 4 ) = 10 ( tuổi )
tuổi bố HN là :
50 - 10 = 40 ( tuổi )
hiệu của hai bố con ko thay đổi nên hiệu vẫn là 30 tuổi
ta có sơ đồ : bố : |----|----|----|
con : |----| hiệu 30 tuổi
tuổi con khi đó là :
30 : ( 3 - 1 ) = 15 ( tuổi )
số năm mà bố gấp 3 tuổi con là :
15 - 10 = 5 ( năm )
ĐS : 5 năm
mình nha

<=> \(\frac{1}{a}+\frac{1}{b}=\frac{1}{a+b+c}-\frac{1}{c}\)
<=>\(\frac{a+b}{ab}=\frac{-\left(a+b\right)}{c\left(a+b+c\right)}\)
<=>c(a+b)(a+b+c)=-ab(a+b)
<=>(a+b)(ac+bc+c2)+ab(a+b)=0
<=>(a+b)(ac+bc+ab+c2)=0
<=>(a+b)(a+c)(c+b)=0
a+b=0
<=> b+c=o
c+a=0

\(\dfrac{1}{a^2+b^2-c^2}+\dfrac{1}{b^2+c^2-a^2}+\dfrac{1}{c^2+a^2-b^2}\)
\(=\dfrac{1}{a^2+b^2-\left(-a-b\right)^2}+\dfrac{1}{b^2+c^2-\left(-b-c\right)^2}+\dfrac{1}{c^2+a^2-\left(-c-a\right)^2}\)
\(=\dfrac{1}{a^2+b^2-\left(a+b\right)^2}+\dfrac{1}{b^2+c^2-\left(b+c\right)^2}+\dfrac{1}{c^2+a^2-\left(c+a\right)^2}\)
\(=\dfrac{1}{a^2+b^2-a^2-2ab-b^2}+\dfrac{1}{b^2+c^2-b^2-2bc-c^2}+\dfrac{1}{c^2+a^2-c^2-2ac-a^2}\)
\(=\dfrac{1}{-2ab}+\dfrac{1}{-2bc}+\dfrac{1}{-2ac}\)
\(=\dfrac{c+a+b}{-2abc}=\dfrac{0}{-2abc}=0\)


Câu 1
\(a+b\ge2\sqrt{ab}\Leftrightarrow ab\le\dfrac{\left(a+b\right)^2}{4}\\ \Leftrightarrow N=ab+\dfrac{1}{16ab}+\dfrac{15}{16ab}\ge2\sqrt{\dfrac{1}{16}}+\dfrac{15}{4\left(a+b\right)^2}\ge\dfrac{1}{2}+\dfrac{15}{4}=\dfrac{17}{4}\)
Dấu \("="\Leftrightarrow a=b=\dfrac{1}{2}\)
Câu 2:
\(P=a+\dfrac{1}{a}+2b+\dfrac{8}{b}+3c+\dfrac{27}{c}+4\left(a+b+c\right)\\ P\ge2\sqrt{1}+2\sqrt{16}+2\sqrt{81}+4\cdot6=2+8+18+4=32\)
Dấu \("="\Leftrightarrow\left\{{}\begin{matrix}a=1\\b=2\\c=3\end{matrix}\right.\)
Câu 3: Cho a,b,c là các số thuộc đoạn [ -1;2 ] thõa mãn \(a^2+b^2+c^2=6.\) CMR : \(a+b+c>0\) - Hoc24

Áp dụng bất đẳng thức Bunhiacopxki dạng phân thức ta có:
\(\dfrac{1}{a}+\dfrac{1}{b}+\dfrac{1}{c}\ge\dfrac{9}{a+b+c}=9\)
Dấu = xảy ra khi a=b=c=1/3
Áp dụng hệ quả bất đẳng thức Cô - si , ta có :
\(\left(\dfrac{1}{a}+\dfrac{1}{b}+\dfrac{1}{c}\right)\left(a+b+c\right)\ge9\)
\(\Leftrightarrow\)\(\left(\dfrac{1}{a}+\dfrac{1}{b}+\dfrac{1}{c}\right)\cdot1\ge9\)
\(\Leftrightarrow\)\(\left(\dfrac{1}{a}+\dfrac{1}{b}+\dfrac{1}{c}\right)\ge9\)