Số cách xếp 4 học sinh vào một dãy ghế dài gồm 10 ghế, mỗi ghế chỉ một học sinh ngồi bằng
A. C 10 4
B. 10 4
C. A 10 4
D. 4 10
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
CM
Cao Minh Tâm
27 tháng 11 2017
Đúng(0)
Những câu hỏi liên quan
CM
26 tháng 7 2018
Chọn D
Chọn 3 học sinh (có thứ tự) xếp vào 10 vị trí có số cách chọn là số chỉnh hợp chập 3 của 10 phần tử: A 10 3
CM
29 tháng 6 2017
Phương pháp:
Xếp lần lượt chỗ ngồi cho từng học sinh nam và nữ sao cho mỗi học sinh nam đều ngồi đối diện với một học sinh nữ. Sử dụng quy tắc nhân.
Cách giải:
Xếp ngẫu nhiên 10 học sinh vào 10 ghế cho 10! cách xếp ⇒ n Ω = 10 !
Gọi A là biến cố: “mỗi học sinh nam đều ngồi đối diện với một học sinh nữ”.
+) Xếp học sinh nam thứ nhất vào 1 trong 10 vị trí cho 10 cách xếp.
Chọn 1 trong 5 bạn nữ xếp ngồi đối diện với bạn nam thứ nhất có 5 cách xếp.
+) Xếp bạn nam thứ 2 vào 1 trong 8 vị trí còn lại có 8 cách xếp.
Chọn 1 trong 4 bạn nữ còn lại xếp ngồi đối diện với bạn nam thứ hai có 4 cách xếp.
+) Xếp bạn nam thứ 3 vào 1 trong 6 vị trí còn lại có 6 cách xếp.
Chọn 1 trong 3 bạn nữ còn lại xếp ngồi đối diện với bạn nam thứ ba có 3 cách xếp.
+) Xếp bạn nam thứ 4 vào 1 trong 4 vị trí còn lại có 4 cách xếp.
Chọn 1 trong 2 bạn nữ còn lại xếp ngồi đối diện với bạn nam thứ tư có 2 cách xếp.
+) Xếp bạn nam thứ 5 vào 1 trong 2 vị trí còn lại có 2 cách xếp.
Xếp 1 bạn nữ còn lại vào vị trí cuối cùng có 1 cách xếp.
CM
30 tháng 9 2017
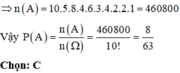
Chọn C
Số phần tử của không gian mẫu: .
Gọi biến cố : “Xếp 10 học sinh vào 10 ghế sao cho mỗi học sinh nam đều ngồi đối diện một học sinh nữ”.
Giả sử đánh vị trí ngồi như bảng sau:
Cách 1: Xếp vị trí A 1 có 10 cách. Mỗi cách xếp vị trí A 1 sẽ có 5 cách xếp vị trí B 1 .
Mỗi cách xếp vị trí A 1 , B 1 có 8 cách xếp vị trí , tương ứng sẽ có 4 cách xếp vị trí B 2 .
Cứ làm như vậy thì số cách xếp thỏa mãn biến cố là:
Cách 2: Đánh số cặp ghế đối diện nhau là C1, C2, C3, C4, C5
Xếp bạn nam vào 5 cặp ghế có 5! cách.
Ở mỗi cặp ghế, ta có 2 cách xếp một cặp nam, nữ ngồi đối diện.
Số phần tử của A là: 
CM
20 tháng 6 2019
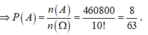
Chọn D
Cách 1. Xếp ngẫu nhiên 10 học sinh vào hai dãy ghế có cách.
Đánh số ghế lần lượt từ 1 đến 10.
Xếp học sinh thỏa mãn bài toán xảy ra hai khả năng sau:
Khả năng 1: Nam ngồi vị trí lẻ, nữ ngồi vị trí chẵn có 5!.5! cách.
Khả năng 2: Nam ngồi vị trí chẵn, nữ ngồi vị trí lẻ có 5!.5! cách.
Vậy có tất cả 2. ( 5 ! ) 2 cách.
Xác suất cần tìm bằng 
Cách 2: Xếp ngẫu nhiên 10 học sinh vào hai dãy ghế, có 10! cách xếp.
Ta chia hai dãy ghế thành 5 cặp ghế đối diện:
+ Chọn 1 nam và 1 nữ xếp vào cặp ghế 1 có 
cách;
+ Chọn 1 nam và 1 nữ xếp vào cặp ghế 2 có 
cách;
+ Chọn 1 nam và 1 nữ xếp vào cặp ghế 3 có 
cách;
+ Chọn 1 nam và 1 nữ xếp vào cặp ghế 4 có 
cách;
+ Chọn 1 nam và 1 nữ xếp vào cặp ghế 5 có 1 cách.
Vậy có tất cả 
cách xếp thỏa mãn.
Xác suất cần tìm bằng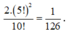 
CM
26 tháng 2 2018
Xếp ngẫu nhiên 10 học sinh có 10! cách. Ta tìm số cách xếp thoả mãn
Đánh số ghế lần lượt từ 1 đến 10.
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
10 |
Nam xếp ghế lẻ, nữ xếp ghế chẵn có 5!5! cách
Nam xếp ghế chẵn, nữ xếp ghế lẻ có 5!5! cách
Vậy có tất cả 5!5!+5!5!cách xếp. Xác suất cần tính bằng 5 ! 5 ! + 5 ! 5 ! 10 ! = 1 126
Chọn đáp án D.
Cách 2: Chia thành 5 cặp ghế đối diện:
Chọn 1 nam và 1 nữ xếp vào cặp ghế 1 có C 5 1 C 5 1 2 ! cách
Chọn 1 nam và 1 nữ xếp vào cặp ghế 2 có C 4 1 C 4 1 cách;
Chọn 1 nam và 1 nữ xếp vào cặp ghế 2 có C 3 1 C 3 1 cách;
Chọn 1 nam và 1 nữ xếp vào cặp ghế 2 có C 2 1 C 2 1 cách;
Cặp nam và nữ còn lại xếp vào cặp ghế 5 có 1 cách.
Vậy có tất cả ( C 5 1 C 4 1 C 3 1 C 2 1 ) 2 2 ! = 2 5 ! 2 cách xếp thoả mãn.
Xác suất cần tính bằng 2 5 ! 2 10 ! = 1 216
Chọn đáp án D.
