Tìm giá trị thực của tham số m để phương trình 9 x - 2 . 3 x + 1 + m = 0 có hai nghiệm thực x 1 , x 2 thỏa mãn x 1 + x 2 = 0
A. m = 6
B. m = 0
C. m = 3
D. m = 1
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Đáp án B.
Đặt t = log2 x,
khi đó m + 1 log 2 2 x + 2 log 2 x + m - 2 = 0
⇔ m + 1 t 2 + 2 t + m - 2 = 0 (*).
Để phương trình (*) có hai nghiệm phân biệt
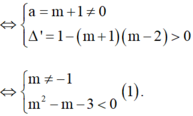
Khi đó gọi x1, x2 lần lượt hai nghiệm của phương trình (*).
Vì 0 < x1 < 1 < x2 suy ra
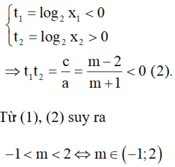

Đáp án C
Với f x > 0 , ∀ x ∈ ℝ . Xét biểu thức f ' x f x = 2 - 2 x *
Lấy nguyên hàm 2 vế (*), ta được ∫ d f x f x = ∫ 2 - 2 x d x
⇔ ∫ d f x f x = - x 2 + 2 x + C ⇔ ln f x = - x 2 + 2 x + C
Mà f(0) =1 suy ra C = lnf(0) = ln1 = 0. Do đó f x = e - x 2 + 2 x
Xét hàm số f x = e - x 2 + 2 x trên - ∞ ; + ∞ , có f ' x = - 2 x + 2 = 0 ⇔ x = 1
Tính giá trị f 1 = e ; lim x → - ∞ f x = 0 ; lim x → - ∞ f x = 0
Suy ra để phương trình f(x) = m có hai nghiệm thực phân biệt ⇔ 0 < m < e .

Trường hợp 1: \(m\ne\pm2\)
Để phương trình có đúng hai nghiệm phân biệt thì phương trình này sẽ có hai nghiệm trái dấu
=>\(m^2-4< 0\)
hay -2<m<2
Trường hợp 2: m=2
Pt sẽ là 1=0(vô lý)
Trường hợp 3: m=-2
=>-4x2+1=0(nhận)
Vậy: -2<=m<2

Bài 2 :
Theo Vi et ta có : \(\hept{\begin{cases}x_1+x_2=-\frac{b}{a}=2\\x_1x_2=\frac{c}{a}=-4\end{cases}}\)
mà \(\left(x_1+x_2\right)^2=4\Rightarrow x_1^2+x_2^2=4+8=12\)
Ta có : \(T=x_1\left(x_1-2x_2\right)+x_2\left(x_2-2x_1\right)\)
\(=x_1^2-2x_2x_1+x_2^2-2x_1x_2=12+16=28\)
Đáp án D