Gọi S là tập tất cả các giá trị thực của tham số m để hàm số y = x 2 + 1 - m x đồng biến trên nửa khoảng [ 3 ; + ∞ ) . Biết rằng S có dạng ( - ∞ ; a ] ∈ ℝ . Trên a 2 ; 2018 a 2 có tất cả bao nhiêu giá trị nguyên?
A. 1816
B. 1815
C. 1914
D. 1913
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

y′=−m2+2m+3(x−m)2′�=−�2+2�+3(�−�)2
Hàm số đồng biến →y′>0→�′>0
→−m2+2m+3>0→−�2+2�+3>0
↔−1<m<3↔−1<�<3
Vì m nguyên nên m� có 33 giá trị.

1.
\(y'=m-3cos3x\)
Hàm đồng biến trên R khi và chỉ khi \(m-3cos3x\ge0\) ; \(\forall x\)
\(\Leftrightarrow m\ge3cos3x\) ; \(\forall x\)
\(\Leftrightarrow m\ge\max\limits_{x\in R}\left(3cos3x\right)\)
\(\Leftrightarrow m\ge3\)
2.
\(y'=1-m.sinx\)
Hàm đồng biến trên R khi và chỉ khi:
\(1-m.sinx\ge0\) ; \(\forall x\)
\(\Leftrightarrow1\ge m.sinx\) ; \(\forall x\)
- Với \(m=0\) thỏa mãn
- Với \(m< 0\Rightarrow\dfrac{1}{m}\le sinx\Leftrightarrow\dfrac{1}{m}\le\min\limits_R\left(sinx\right)=-1\)
\(\Rightarrow m\ge-1\)
- Với \(m>0\Rightarrow\dfrac{1}{m}\ge sinx\Leftrightarrow\dfrac{1}{m}\ge\max\limits_R\left(sinx\right)=1\)
\(\Rightarrow m\le1\)
Kết hợp lại ta được: \(-1\le m\le1\)

Chọn D.
![]()
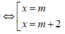
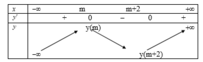
Do đó ta có bảng biến thiên sau:
Để hàm số nghịch biến trên khoảng (-1;1) thì
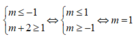
Đáp án A
BBT