a) Vẽ đường thẳng đi qua hai điểm A và B.
b) Lấy điểm C để có ba điểm A, B, C thẳng hàng.

Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

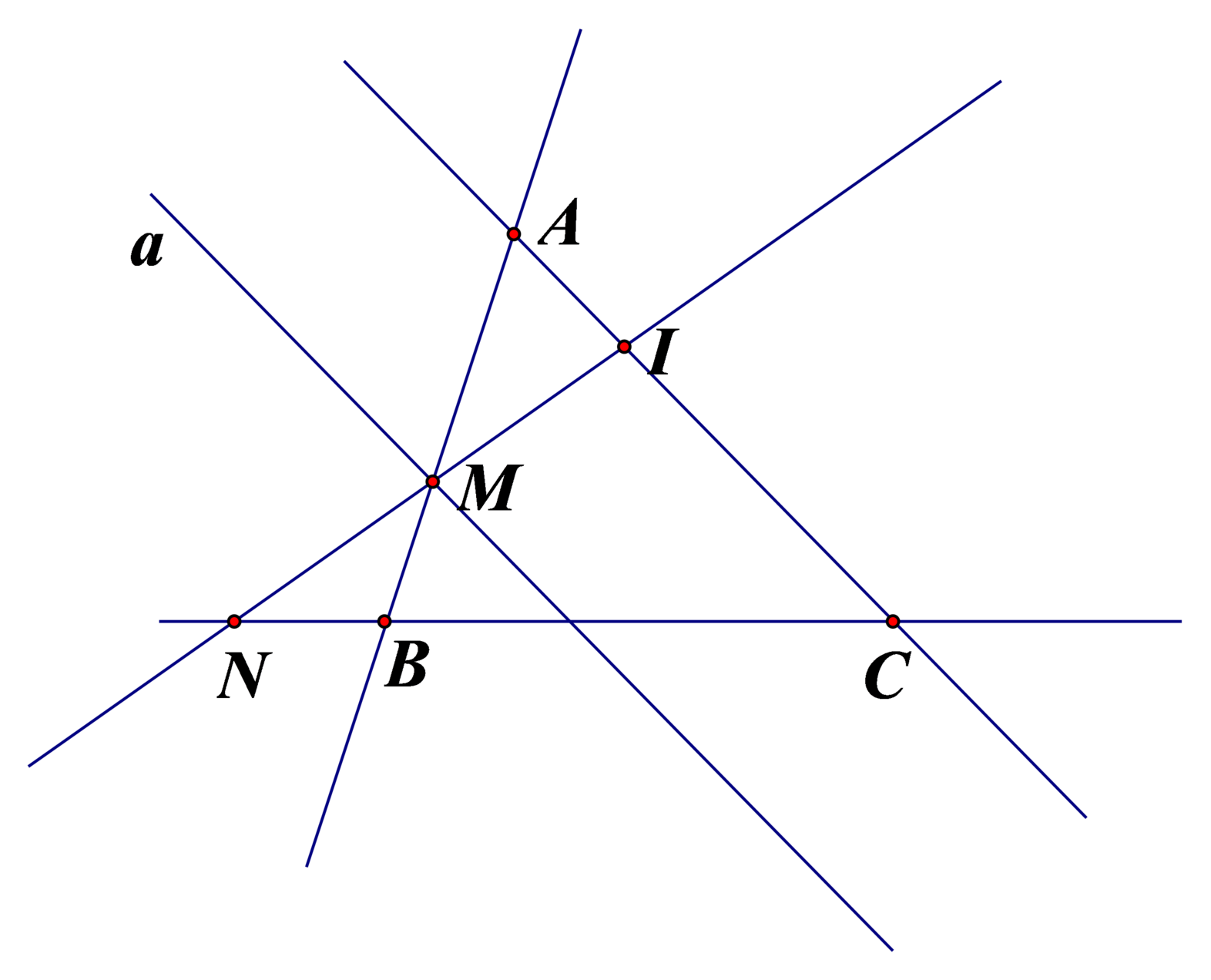
I là giao điểm của đường thẳng AC
Và đường thẳng MN thì ba điểm I, M, N thẳng hàng.

Phương pháp giải:
Vận dụng kiến thức về ba điểm thẳng hàng, vẽ theo yêu cầu của bài toán.
Lời giải chi tiết:
a) Đi qua hai điểm M, N

Chấm thêm một điểm P để M, N, P thẳng hàng.
b) Đi qua điểm O
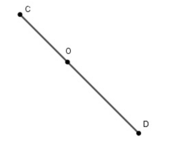
Chấm thêm 2 điểm C và D để C, O, D thẳng hàng.
c) Đi qua hai trong ba điểm A, B, C.
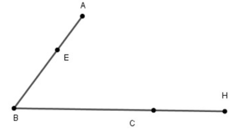
Chấm thêm hai điểm E và H để A, E, B thẳng hàng và B, C, H thẳng hàng.

Lời giải:
a. Gọi ptdt $(d)$ đi qua $A,B$ là $y=ax+b$
Ta có: \(\left\{\begin{matrix} y_A=ax_A+b\\ y_B=ax_B+b\end{matrix}\right.\Leftrightarrow \left\{\begin{matrix} 2=a+b\\ 1=a.0+b\end{matrix}\right.\Leftrightarrow \left\{\begin{matrix} b=1\\ a=1\end{matrix}\right.\)
Vậy ptđt $(d)$ là: $y=x+1$
b. Ta thấy: $y_C=-4=-5+1=x_C+1$ nên $C\in (d): y=x+1$
Tức là $C$ thuộc đt đi qua 2 điểm $A,B$
$\Rightarrow A,B,C$ thẳng hàng.

đừng ghi a,b,c mình vẽ trong hình vào mk ghi lộn
trên hình vẽ có 6 đường thẳng : AB,AD,BD,CB,CD,AC
có 3 đường thẳng trùng nhau : AD,DB trùng với AB
Đường thẳng m cắt đường thẳng CA,CD,CB
giao điểm của đường thẳng m với CA là A,CD là D,CB là B
D là giao điểm của m và CD,AD và DB

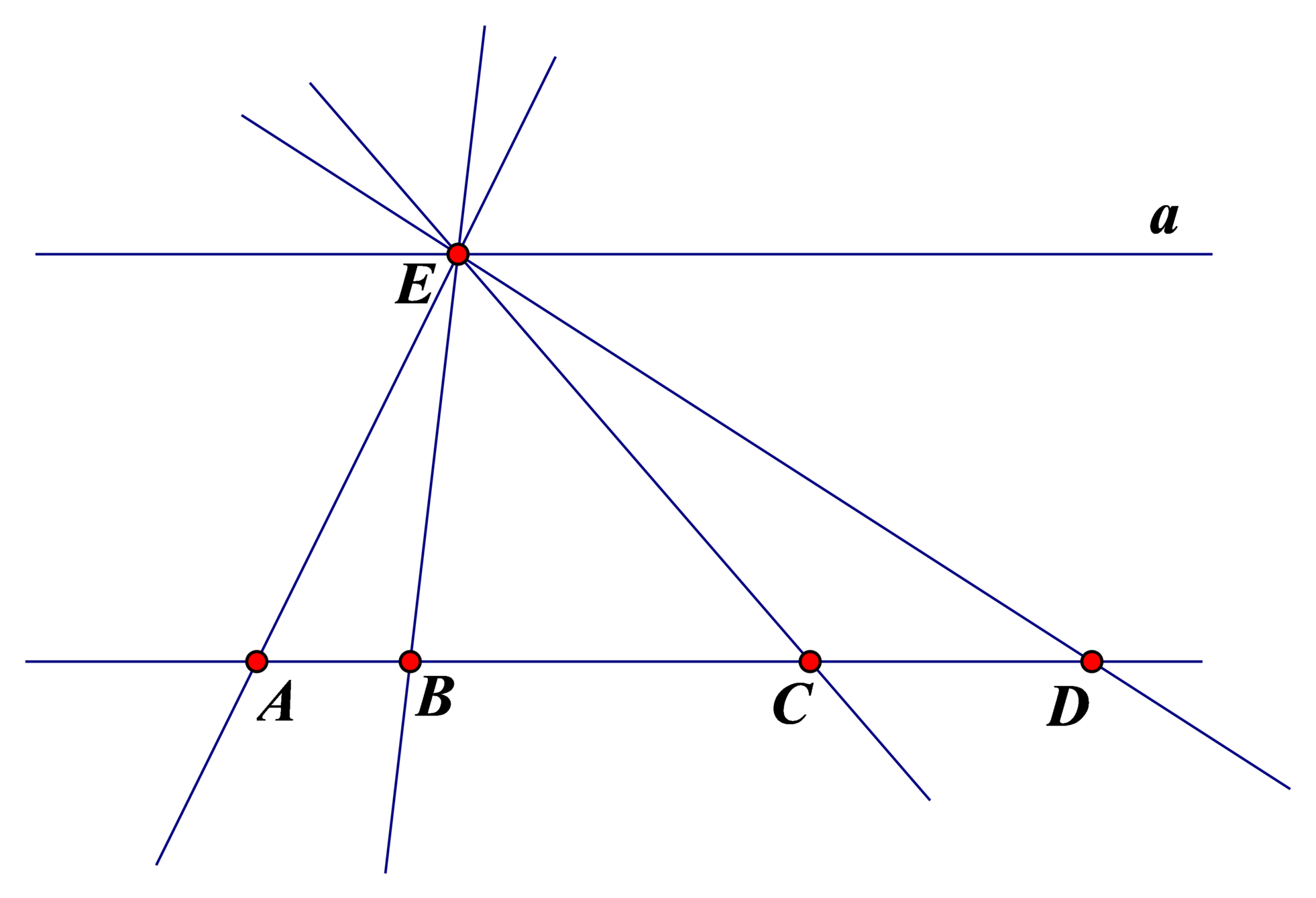
- Có năm đường thảng phân biệt trong hình vẽ, đó là: EA , EB , EC , ED , AB .
- Hai đường thẳng AB và CD trùng nhau; đường thẳng a song song với đường thẳng AB nên cũng song song với đường thẳng CD. Do đó, đường thẳng a không cắt đường thẳng CD.
Phương pháp giải:
- Dùng thước và bút chì, kẻ đường thẳng đi qua hai điểm A và B.
- Lấy điểm C sao cho C nằm trên đường thẳng AB vừa vẽ.
Lời giải chi tiết:
a) Vẽ đường thẳng đi qua hai điểm A và B.
b) Lấy điểm C để có ba điểm A, B, C thẳng hàng.