Cho tam giác ABC có ba đường cao AD, BE, CF cắt nhau tại H. Biết ba góc CAB ^ , ABC ^ , BCA ^ đều là góc nhọn. Gọi M là trung điểm của đoạn AH.
1) Chứng minh tứ giác AEHF nội tiếp đường tròn.
2) Chứng minh CE.CA = CD.CB.
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

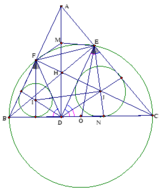
3) Chứng minh EM là tiếp tuyến của đường tròn ngoại tiếp tam giác BEF
Tứ giác BFEC có B E C ^ = B F C ^ = 90 0
=> tứ giác BFEC nội tiếp đường tròn đường kính BC
Gọi O là tâm đường tròn ngoại tiếp tứ giác BFEC thì O cũng là tâm đường tròn ngoại tiếp tam giác BEF
∆ OBE cân tại O (do OB=OE) => O B E ^ = O E B ^
∆ AEH vuông tại E có EM là trung tuyến ứng với cạnh huyền AH (Vì M là trung điểm AH)
=> ME=AH:2= MH do đó ∆ MHE cân tại M=> M E H ^ = M H E ^ = B H D ^
Mà B H D ^ + O B E ^ = 90 0 ( ∆ HBD vuông tại D)
Nên O E B ^ + M E H ^ = 90 0 Suy ra M E O ^ = 90 0
⇒ E M ⊥ O E tại E thuộc ( O ) => EM là tiếp tuyến của đường tròn ngoại tiếp tam giác BEF
4) Gọi I và J tương ứng là tâm đường tròn nội tiếp hai tam giác BDF và EDC. Chứng minh DIJ ^ = DFC ^
Tứ giác AFDC có A F C ^ = A D C ^ = 90 0 nên tứ giác AFDC nội tiếp đường tròn => B D F ^ = B A C ^
∆ BDF và ∆ BAC có B D F ^ = B A C ^ (cmt); B ^ chung do đó ∆ BDF ~ ∆ BAC(g-g)
Chứng minh tương tự ta có ∆ DEC ~ ∆ ABC(g-g)
Do đó ∆ DBF ~ ∆ DEC ⇒ B D F ^ = E D C ^ ⇒ B D I ^ = I D F ^ = E D J ^ = J D C ^ ⇒ I D J ^ = F D C ^ (1)
Vì ∆ DBF ~ ∆ DEC (cmt); DI là phân giác, DJ là phân giác ⇒ D I D F = D J D C (2)
Từ (1) và (2) suy ra ∆ DIJ ~ ∆ DFC (c-g-c) => DIJ ^ = DFC ^

a) Dễ thấy A, H, K thẳng hàng.
Ta có \(\widehat{KCB}=\widehat{HCB}=90^o-\widehat{ABC}=\widehat{KAB}\).
Suy ra tứ giác ACKB nội tiếp.
b) \(\widehat{ABD}=\widehat{AA'C};\widehat{ADB}=\widehat{ACA'}=90^o\Rightarrow\Delta ABD\sim\Delta AA'C\left(g.g\right)\Rightarrow\widehat{BAD}=\widehat{A'AC}\)
\(\Rightarrow\widehat{AA'C}=90^o-\widehat{ABC}=90^o-\widehat{AEF}\Rightarrow AA'\perp EF\)
c) Ta có BH // A'C (do cùng vuông góc với AC), CH // A'B (do cùng vuông góc với AB) nên tứ giác BHCA' là hình bình hành. Suy ra H, I, A' thẳng hàng.
d) Do OI là đường trung bình của tam giác A'AH nên OI // AH,\(\dfrac{OI}{AH}=\dfrac{1}{2}=\dfrac{IG}{AG}\Rightarrow\) H, G, O thẳng hàng và \(\dfrac{OG}{HG}=\dfrac{1}{2}\). Từ đó \(S_{AHG}=2S_{AOG}\) (đpcm)

a: góc HBC+góc HCB=90 độ-góc ACB+90 độ-góc ABC=góc BAC
=>góc BHC+góc BAC=180 độ
H đối xứng K qua BC
=>BH=BK và CH=CK
Xét ΔBHC và ΔBKC có
BH=BK
CH=CK
BC chung
=>ΔBHC=ΔBKC
=>góc BKC=góc BHC
=>góc BKC+góc BAC=180 độ
=>ABKC nội tiếp
b: Gọi Ax là tiếp tuyến của (O) tại A
=>góc xAC=góc ABC=góc AEF
=>EF//Ax
=>EF vuông góc OA
c: Xét tứ giác BHCA' có
BH//CA'
BA'//CH
=>BHCA' là hbh
=>H,I,A' thẳng hàng

a: góc AEH+góc AFH=180 độ
=>AEHF nội tiếp
b: góc DFC=góc EBC
góc EFC=góc DAC
góc EBC=góc DAC
=>góc DFC=góc EFC

1) Ta có: BH vuông góc với AC
CK vuông góc với AC
=> BH//CK
Chứng minh tương tự ta có: CH//Bk
Xét tứ giác BHCK có: BH//CK
CH//BK
=> Tứ giác BHCK là hbh
Có M là trung điểm của BC=> M là trung điểm của HK=>M,H,K thẳng hàng
2.gọi HI cắt BC tại J
Xét tam giác HIK có: J là trung điểm của HI
M là trung điểm của HK
=> JM là đường trung bình trong tam giác HIK
=> IK//MJ hay IK//BC
Xét tam giác BHJ và tam giác BIJ có;
HJ=JI
góc BJH=góc BJI=90
BJ chung
=> Tam giác BHJ = tam giác BIJ
=> Góc HBJ= góc IBJ
Mà góc HBJ= góc BCK( do BH//CK)
Xét tứ giác BIKC có:
KI//BC
góc IBC= góc KCB
=>Tứ giác BIKC là hình thang cân
3.Xét tứ giác GHCK có: GK//HC (doBK//HC)
=> Tứ giác GHCK là hình thang
Để GHCK là hình thang cân<=>góc GHC= góc KCH(1)
mà GHC+HCB=90
KCH+HCA=90
=> (1)<=> góc HCB=góc HCA=> CH là phân giác của góc ACB
Xét tam giác ABC có : CH là phân giác của góc ACB
CH là đường cao trong tam giác ABC
=> Tam giác ABC cân tại C
Vậy tứ giác GHCK là hình thang cân<=> Tam giác ABC cân tại C

1) Chứng minh tứ giác AEHF nội tiếp đường tròn
BE là đường cao ∆ ABC ⇒ B E ⊥ A C ⇒ A E H ^ = 90 0
CF là đường cao ∆ ABC ⇒ C F ⊥ A B ⇒ A F H ^ = 90 0
Tứ giác AEHF có A E H ^ + A F H ^ = 180 0 nên tứ giác AEHF nội tiếp đường tròn
2) Chứng minh CE.CA = CD.CB
∆ ADC và ∆ BEC có
A D C ^ = B E C ^ = 90 0 (AD,BE là các đường cao)
C ^ chung
Do đó ∆ ADC ~ ∆ BEC(g-g)
⇒ D C E C = A C B C ⇒ D C . B C = C E . A C