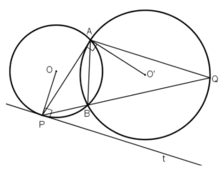
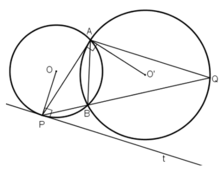
Cho hai đường tròn (O; R) và (O'; r) tiếp xúc ngoài với nhau tại A. Vẽ tiếp tuyến chung ngoài BC với B ∈ (O), C ∈ (O'). Đường vuông góc với OO' kẻ từ A cắt BC ở M
a, Tính MA theo R và r
b, Tính diện tích tứ giác BCO'O theo R và r
c, Tính diện tích ∆BAC theo R và r
d, Gọi I là trung điểm của OO'. Chứng minh rằng BC là tiếp tuyến của đường tròn (I; IM)


 ΔPBO
ΔPBO

 ΔPBO
ΔPBO




a, Chứng minh được tương tự câu 1a,
=> O ' M O ^ = 90 0
Áp dụng hệ thức lượng trong tam giác vuông tính được MA = R r
b, Chứng minh S B C O O ' = R + r R r
c, Chứng minh được: ∆BAC:∆OMO’ => S B A C S O M O ' = B C O O ' 2
=> S B A C = S O M O ' . B C 2 O O ' 2 = 4 R r R r R + r
d, Tứ giác OBCO’ là hình thang vuông tại B và C có IM là đường trung bình => IM ⊥ BC = {M}