Đưa các phương trình sau về dạng ax2 + 2b'x + c = 0 và giải chúng. Sau đó, dùng bảng số hoặc máy tính để viết gần đúng nghiệm tìm được (làm tròn kết quả đến chữ số thập phân thứ hai): 0,5x(x + 1) = (x – 1)2
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


3x2 + 3 = 2(x + 1)
⇔ 3x2 + 3 = 2x + 2
⇔ 3x2 + 3 – 2x – 2 = 0
⇔ 3x2 – 2x + 1 = 0
Phương trình có a = 3; b’ = -1; c = 1; Δ’ = b’2 – ac = (-1)2 – 3.1 = -2 < 0
Vậy phương trình vô nghiệm.

(2x - √2)2 – 1 = (x + 1)(x – 1);
⇔ 4x2 – 2.2x.√2 + 2 – 1 = x2 – 1
⇔ 4x2 – 2.2√2.x + 2 – 1 – x2 + 1 = 0
⇔ 3x2 – 2.2√2.x + 2 = 0
Có: a = 3; b’ = -2√2; c = 2; Δ’ = b’2 – ac = (-2√2)2 – 3.2 = 2 > 0
Vì Δ’ > 0 nên phương trình có hai nghiệm phân biệt là:
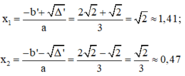

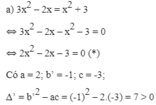
Phương trình (*) có hai nghiệm phân biệt:
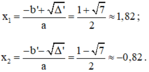

Có: a = 3; b’ = -2√2; c = 2;
Δ ’ = b ’ 2 – a c = ( - 2 √ 2 ) 2 – 3 . 2 = 2 > 0
Vì Δ’ > 0 nên phương trình có hai nghiệm phân biệt là:
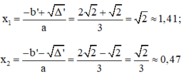
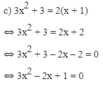
Phương trình có a = 3; b’ = -1; c = 1;
Δ ’ = b ’ 2 – a c = ( - 1 ) 2 – 3 . 1 = - 2 < 0
Vậy phương trình vô nghiệm.
d)
0 , 5 x ( x + 1 ) = ( x – 1 ) 2 ⇔ 0 , 5 x 2 + 0 , 5 x = x 2 – 2 x + 1 ⇔ x 2 – 2 x + 1 – 0 , 5 x 2 – 0 , 5 x = 0 ⇔ 0 , 5 x 2 – 2 , 5 x + 1 = 0 ⇔ x 2 – 5 x + 2 = 0
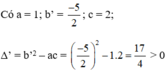
Phương trình có hai nghiệm phân biệt:
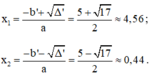

3x2 – 2x = x2 + 3
⇔ 3x2 – 2x – x2 – 3 = 0
⇔ 2x2 – 2x – 3 = 0 (*)
Có a = 2; b’ = -1; c = -3; Δ’ = b’2 – ac = (-1)2 – 2.(-3) = 7 > 0
Phương trình (*) có hai nghiệm phân biệt:
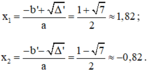

Bài giải:
a) 3x2 – 2x = x2 + 3 ⇔ 2x2 – 2x - 3 = 0.
b’ = -1, ∆’ = (-1)2 – 2 . (-3) = 7
x1 = ≈ 1, 82; x2 =
≈ -0,82
b) (2x - √2)2 – 1 = (x + 1)(x – 1) ⇔ 3x2 - 4√2 . x + 2 = 0 . b’ = -2√2
∆’ = (-2√2)2 – 3 . 2 = 2
x1 = = √2 ≈ 1,41; x2 =
=
≈ 0,47.
c) 3x2 + 3 = 2(x + 1) ⇔ 3x2 – 2x + 1 = 0.
b’ = -1; ∆’ = (-1)2 – 3 . 1 = -2 < 0
Phương trình vô nghiệm.
d) 0,5x(x + 1) = (x – 1)2 ⇔ 0,5x2 – 2,5x + 1 = 0
⇔ x2 – 5x + 2 = 0, b’ = -2,5; ∆’ = (-2,5)2 – 1 . 2 = 4,25
x1 = 2,5 + √4,25 ≈ 4,56, x2 = 2,5 - √4,25 ≈ 0,44
(Rõ ràng trong trường hợp này dung công thức nghiệm thu gọn cũng không đơn giản hơn)
a) 3x2 – 2x = x2 + 3 ⇔ 2x2 – 2x - 3 = 0.
b’ = -1, ∆’ = (-1)2 – 2 . (-3) = 7
x1 = ≈ 1, 82; x2 =
≈ -0,82
b) (2x - √2)2 – 1 = (x + 1)(x – 1) ⇔ 3x2 - 4√2 . x + 2 = 0 . b’ = -2√2
∆’ = (-2√2)2 – 3 . 2 = 2
x1 = = √2 ≈ 1,41; x2 =
=
≈ 0,47.
c) 3x2 + 3 = 2(x + 1) ⇔ 3x2 – 2x + 1 = 0.
b’ = -1; ∆’ = (-1)2 – 3 . 1 = -2 < 0
Phương trình vô nghiệm.
d) 0,5x(x + 1) = (x – 1)2 ⇔ 0,5x2 – 2,5x + 1 = 0
⇔ x2 – 5x + 2 = 0, b’ = -2,5; ∆’ = (-2,5)2 – 1 . 2 = 4,25
x1 = 2,5 + √4,25 ≈ 4,56, x2 = 2,5 - √4,25 ≈ 0,44

( 3 - x 5 )(2x 2 + 1) = 0 ⇔ 3 - x 5 = 0 hoặc 2x 2 + 1 = 0
3 - x 5 = 0 ⇔ x = 3 / 5 ≈ 0,775
2x 2 + 1 = 0 ⇔ x = - 1/2 2 ≈ - 0,354
Phương trình có nghiệm x = 0,775 hoặc x = - 0,354

(2x - 7 )(x 10 + 3) = 0 ⇔ 2x - 7 = 0 hoặc x 10 + 3 = 0
2x - 7 = 0 ⇔ x = 7 /2 ≈ 1,323
x 10 + 3 = 0 ⇔ x = - 3/ 10 ≈ - 0,949
Phương trình có nghiệm x = 1,323 hoặc x = - 0,949

(2 – 3x 5 )(2,5x + 2 ) = 0 ⇔ 2 – 3x 5 = 0 hoặc 2,5x + 2 = 0
2 – 3x 5 = 0 ⇔ x = 2/3 5 ≈ 0,298
2,5x + 2 = 0 ⇔ x = - 2 / (2,5) ≈ - 0,566
Phương trình có nghiệm x = 0,298 hoặc x = - 0,566

(x 2 , 7 – 1,54)( 1 , 02 + x 3 , 1 ) = 0
⇔ x 2 , 7 – 1,54 = 0 hoặc 1 , 02 + x 3 , 1 = 0
x 2 , 7 – 1,54 = 0 ⇔ x = 1,54/ 2 , 7 ≈ 0,94
1 , 02 + x 3 , 1 = 0 ⇔ x = - 1 , 02 / 3 , 1 ≈ - 0,57
Vậy phương trình có nghiệm x = 0,94 hoặc x = - 0,57.
0,5x(x + 1) = (x – 1)2
⇔ 0,5x2 + 0,5x = x2 – 2x + 1
⇔ x2 – 2x + 1 – 0,5x2 – 0,5x = 0
⇔ 0,5x2 – 2,5x + 1 = 0
⇔ x2 – 5x + 2 = 0
Phương trình có hai nghiệm phân biệt: