Cho hai đường tròn (O) và (O') cắt nhau tại A và B. Gọi M là trung điểm của OO'. Đường thẳng qua A cắt các đường tròn (O) và (O’) lần lượt ở C và D
a, Khi CD ⊥ MA, chứng minh AC = AD
b, Khi CD đi qua A và không vuông góc với MA
i, Vẽ đường kính AE của (O), AE cắt (O’) ở H. Vẽ đường kính AF của (O'), AF cắt (O) ở G. Chứng minh AB, EG, FH đồng quy
ii, Tìm vị trí của CD để đoạn CD có độ dài lớn nhất?


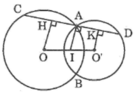
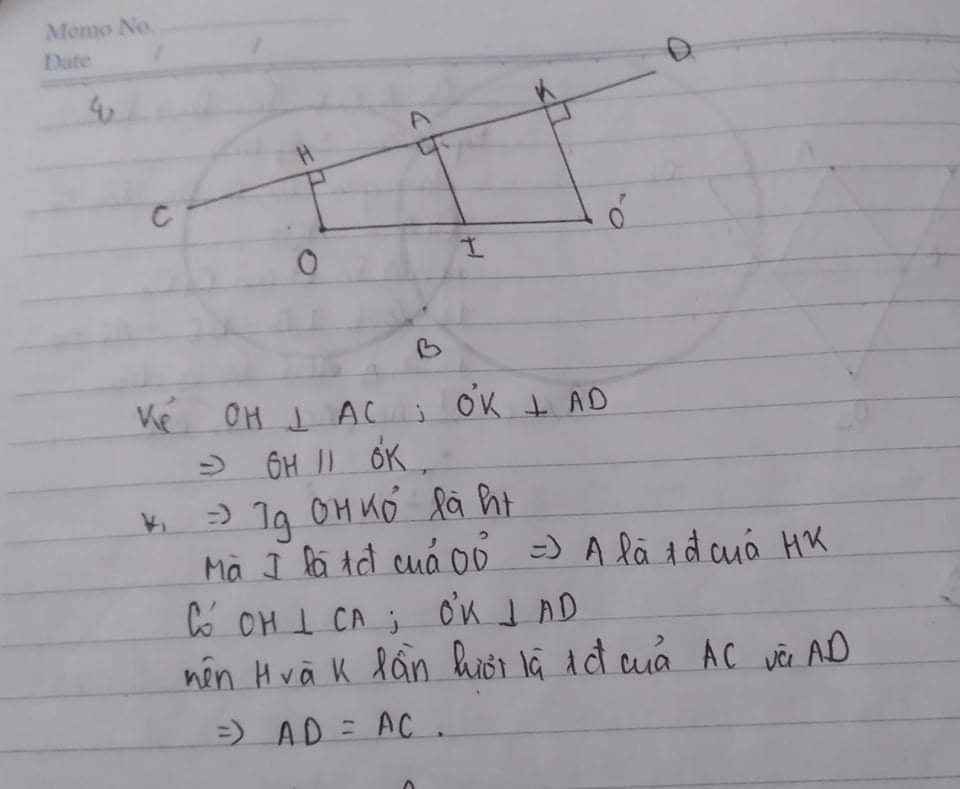
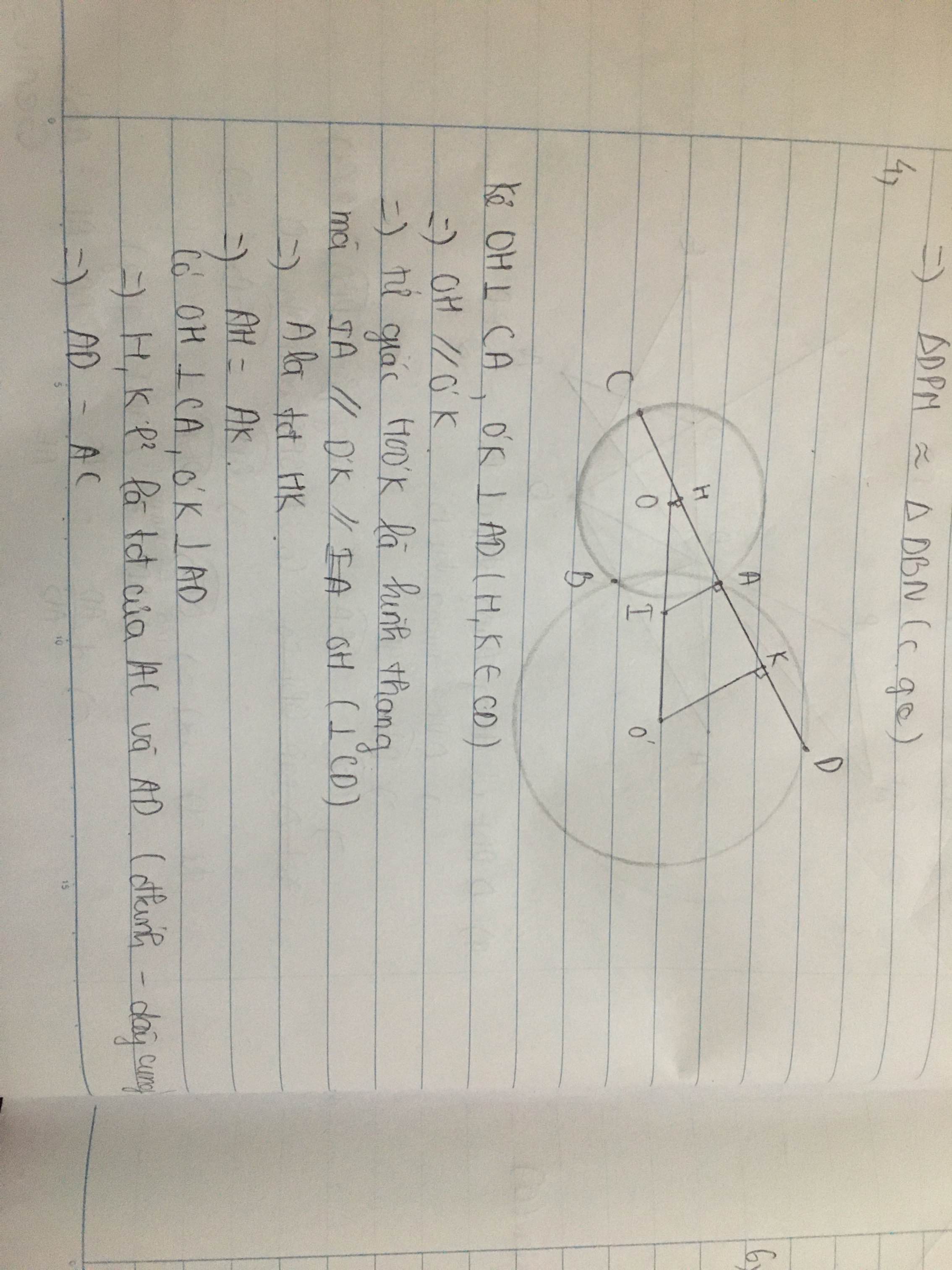
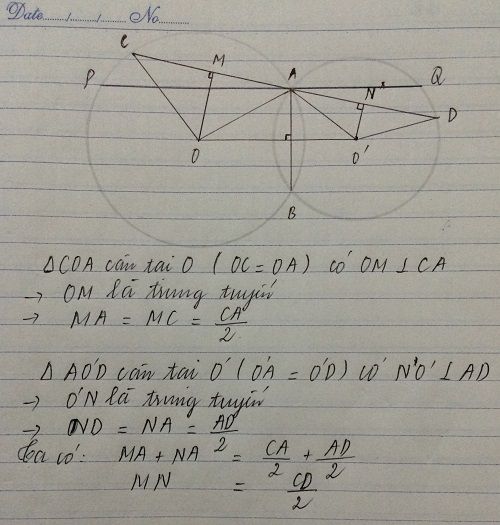
Vẽ OP ⊥ CA; O’Q ⊥ AD suy ra tứ giác OPQO’ là hình thang vuông tại P, Q
a, Kẻ OP; O’Q ⊥ CD do CD ⊥ MA và M là trung điểm của OO’ => AP=AQ => AC=AD
b,i, Chú ý ∆EAF có AB, EG,FI là ba đường cao
ii, Sử dụng CD= 2PQ để lập luận, ta có
Kết luận: CD lớn nhất khi CD//OO’