Cho tam giác ABC có a = 5, b = 7, c = 8. Bán kính đường tròn ngoại tiếp tam giác bằng
A. 7 3
B. 7 3 3
C. 7 5 3
D. 7 2 3
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

ửa chu vi tam giác: p = 7 + 8 + 9 2 = 12
Áp dụng công thức Hê- rông, diện tích tam giác ABC
S = 12 12 − 7 12 − 8 12 − 9 = 12.5.4.3 = 12 5
Bán kính đường tròn nội tiếp của tam giác là r = S p = 12 5 12 = 5
ĐÁP ÁN C

a)
– Tọa độ trọng tâm G của tam giác ABC là:
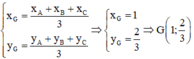
– Tọa độ trực tâm H của tam giác ABC:
Cách 1:
+ Phương trình đường cao BD:
BD ⊥ AC ⇒ Đường thẳng BD nhận 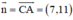 là một vtpt
là một vtpt
BD đi qua B(2; 7)
⇒ Phương trình đường thẳng BD: 7(x - 2) +11(y - 7) = 0 hay 7x + 11y – 91 = 0
+ Phương trình đường cao CE:
CE ⊥ AB ⇒ Đường thẳng CE nhận 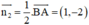 là một vtpt
là một vtpt
CE đi qua C(–3; –8)
⇒ Phương trình đường thẳng CE: 1(x + 3) – 2(y + 8)=0 hay x – 2y – 13 = 0.
Trực tâm H là giao điểm của BD và CE nên tọa độ của H là nghiệm của hpt:
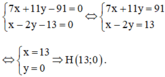
Cách 2: Gọi H(x, y) là trực tâm tam giác ABC
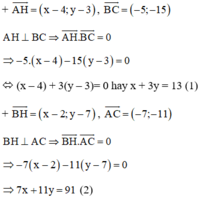
Từ (1) và (2) ta có hệ phương trình
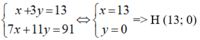
b) Gọi T(x; y) là tâm đường tròn ngoại tiếp tam giác ABC
Khi đó TA = TB = TC = R.
+ TA = TB ⇒ AT2 = BT2
⇒ (x – 4)2 + (y – 3)2 = (x – 2)2 + (y – 7)2
⇒ x2 – 8x + 16 + y2 – 6y + 9 = x2 – 4x + 4 + y2 – 14y + 49
⇒ 4x – 8y = –28
⇒ x – 2y = –7 (1)
+ TB = TC ⇒ TB2 = TC2
⇒ (x – 2)2 + (y – 7)2 = (x + 3)2 + (y + 8)2
⇒ x2 – 4x + 4 + y2 – 14y + 49 = x2 + 6x + 9 + y2 + 16y + 64
⇒ 10x + 30y = –20
⇒ x + 3y = –2 (2)
Từ (1) và (2) ⇒ x = –5, y = 1 ⇒ T(–5 ; 1).
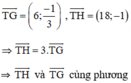
⇒ T, H, G thẳng hàng.
c) Tâm đường tròn ngoại tiếp ΔABC: T(–5; 1)
Bán kính đường tròn ngoại tiếp ΔABC:
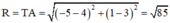
Vậy phương trình đường tròn ngoại tiếp tam giác ABC:
(x + 5)2 + (y – 1)2 = 85

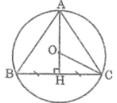
Vì O là tâm đường tròn ngoại tiếp tam giác ABC nên O là giao điểm của ba đường trung trực trong tam giác ABC.
Kẻ AH ⊥ BC. Ta có: O ∈ AH
Trong tam giác vuông ABH, ta có:
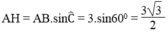
Vì tam giác ABC đều nên AH là đường cao cũng đồng thời là trung tuyến nên:
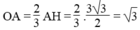
Vậy chọn đáp án C.

a 2 + b 2 = 5 2 + 12 2 = 13 2 ⇒ a 2 + b 2 = c 2 ⇒ ∆ABC vuông tại C
Bán kính đường tròn ngoại tiếp tam giác ABC là R = c 2 = 13 2 = 6,5 .
Chọn C.

Đáp án A.
Gọi K(a;b) là tâm đường tròn ngoại tiếp Δ A B C .
Ta có: A K 2 = a - 1 2 + b - 2 2 ; B K 2 = a - 5 2 + b - 4 2 và
C K 2 = a - 3 2 + b + 2 2 .
Từ A K 2 = B K 2 = C K 2 , ta có a - 1 2 + b - 2 2 = a - 5 2 + b - 4 2 a - 1 2 + b - 2 2 = a - 3 2 + b + 2 2
⇔ - 2 a - 4 b + 5 = - 10 a - 8 b + 41 - 2 a - 4 b + 5 = - 6 a + 4 b + 13 ⇔ 2 a + b = 9 a - 2 b = 2 ⇔ a = 4 b = 1 → K 4 ; 1 .
Bán kính đường tròn ngoại tiếp ∆ A B C là R = A K = 4 - 1 2 + 1 - 2 2 = 10 .
Gọi K' là tâm đường tròn ngoại tiếp ∆ A ' B ' C ' , do V 1 ; - 3 = ∆ A B C = ∆ A ' B ' C ' nên V 1 ; - 3 K = K ' → I K → = - 3 I K → . Mà V 1 ; - 3 A = A ' → I A → = - 3 I A → .
Suy ra I A ' → - I K ' → = - 3 I A → - I K → ⇔ K ' A ' → = - 3 K A → . Bán kính đường tròn ngoại tiếp ∆ A ' B ' C ' là R = K ' A ' = 3 K A = 3 R = 3 10 .
Nửa chu vi tam giác p = 5 + 7 + 8 2 = 10
Áp dụng công thức Hê- rông, diện tích tam giác ABC
S = 10 10 − 5 10 − 7 10 − 8 = 10 3
Bán kính đường tròn ngoại tiếp tam giác:
R = a b c 4 S = 5.7.8 40 3 = 7 3 3
ĐÁP ÁN B.