Bất phương trình ax + b > 0 vô nghiệm khi
A. a ≠ 0 b = 0
B. a > 0 b > 0
C. a = 0 b ≠ 0
D. a = 0 b ≤ 0
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Nếu a > 0 thì ax + b > 0 ⇔ x > - b/a nên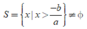
Nếu a < 0 thì ax + b > 0 ⇔ x < - b/a nên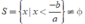
Nếu a = 0 thì ax + b > 0 có dạng 0x + b > 0
Với b > 0 thì S = R.
Với b ≤ 0 thì S = Ø
Chọn đáp án D.

Nếu a > 0 thì ax + b ≤ 0 ⇔ x ≤ - b/a nên S ≠ Ø
Nếu a < 0 thì ax + b ≤ 0 ⇔ x ≥ - b/a nên S ≠ Ø
Nếu a = 0 thì ax + b ≤ 0 có dạng 0x + b ≤ 0
Với b ≤ 0 thì S = R.
Với b > 0 thì S = Ø
Chọn đáp án A.

uses crt;
var a, b: logint;
Begin
write('nhap so a ='); Readln(a);
write('nhap so b ='); readln(b);
If (a = 0 and b = 0)
then write ('pt co nghiem x thuoc R')
else
if (a=0 and b#0) then write('pt vo nghiem')
else
write(nghiẹm la x=': -b/a);
readln
end.
uses crt;
var a, b: logint;
Begin
write('nhap so a ='); Readln(a);
write('nhap so b ='); readln(b);
If (a = 0 and b = 0)
then write ('pt co nghiem x thuoc R')
else
if (a=0 and b#0) then write('pt vo nghiem')
else
write(nghiẹm la x=': -b/a);
readln
end.

Hệ phương trình a x + b y = c a ' x + b ' y = c ' có vô số nghiệm khi d: ax + by = c và d’: a’x + b’y = c’ trùng nhau, suy ra hệ phương trình có vô số nghiệm ⇔ a a ' = b b ' = c c '
Đáp án: B

Các giải của các bài toán này là sử dụng tổng các delta em nhé

Xét phương trình bậc hai ax2 + bx + c = 0 (a ≠ 0)
với b = 2b’ và biệt thức Δ ' = b ' 2 − a c
Trường hợp 1: Nếu Δ ' < 0 thì phương trình vô nghiệm
Trường hợp 2: Nếu Δ ' = 0 thì phương trình có nghiệm kép x1 = x2 = − b ' a
Trường hợp 3: nếu Δ ' > 0 thì phương trình có hai nghiệm phân biệt
x1,2 = − b ' ± Δ ' a
Đáp án cần chọn là: D

Ta có:
\(\Delta_1+\Delta_2+\Delta_3=a^2-4b+b^2-4c+c^2-4a=a^2+b^2+c^2-48\)
Dễ thấy:\(a^2+b^2+c^2\ge\frac{\left(a+b+c\right)^2}{3}=48\Rightarrow\Delta_1+\Delta_2+\Delta_3\ge0\)
Khi đó có ít nhất một phương trình có nghiệm

PT vô nghiệm <=> 0 < a < b
=> c > 0 và 4ac > b2
=> 4ac - 2bc + c2 > b2 - 2bc + c2 = (b - c)2
=> 4ac - 2bc + c2 > 0
=> 4a - 2b + c > 0
=> a + b + c > -3a + 3b
=> (a + b + c)/(b - a) > 3 (ĐPCM)
Nếu a > 0 thì ax + b > 0 ⇔ x > - b/a nên
Nếu a < 0 thì ax + b > 0 ⇔ x < - b/a nên
Nếu a = 0 thì ax + b > 0 có dạng 0x + b > 0
Với b > 0 thì S = R.
Với b ≤ 0 thì S = Ø
Chọn đáp án D.