Cho e π m < e π n . Khi đó
A. m ≤ n
B. m > n
C. m = n
D. m < n
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
CM
25 tháng 3 2017
Các số có căn bậc hai:
a = 0 c = 1 d = 16 + 9
e = 32 + 42 h = (2-11)2 i = (-5)2
l = √16 m = 34 n = 52 - 32
Căn bậc hai không âm của các số đó là:
T
27 tháng 6 2016
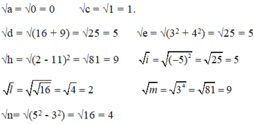
x,x+1,x+2 chó x là 1 thì bàng 1,1+1,1+2+1,2,3 đúng
b-1,b,b+1 cho b là 1 thì bàng 1-1,1,1+1=0,1,2 đúng
chỉ có 2 câu này đúng thoy
còn 2 câu kia sai oke
với lại chữ E đó là sao vậy
HD
Hà Đức Thọ
Admin
12 tháng 1 2018
Đây là một câu hỏi rất rộng. Để biết khi nào dùng đạo hàm, nguyên hàm, ... thì bạn cần phải học về khái niệm của các đại lượng trên, cách tính và ý nghĩa của nó như thế nào.
Ví dụ về đạo hàm chẳng hạn.
Người ta định nghĩa đạo hàm thế này:
Hàm số \(y=f(x)\) xác định trên tập \(D\)
Tại giá trị \(x=x_0\) thì \(y=y_0\)
Tại giá trị \(x=x_1\) thì \(y=y_1\)
Ta có biến thiên của hàm số là: \(\Delta y=y_1-y_0\)
Biến thiên của đối số là: \(\Delta x = x_1-x_0\)
Ta gọi giới hạn nếu có của tỉ số \(\dfrac{\Delta y}{\Delta x}\) khi \(\Delta x\) tiến đến 0 là đạo hàm bậc nhất của hàm số \(y=f(x)\) tại \(x=x_0\)
Viết là: \(y'=\lim\limits_{\Delta x\rightarrow0}\dfrac{\Delta y}{\Delta x}\)
Ý nghĩa của đạo hàm
Trong chuyển động thẳng không đều, khi gắn chuyển động vào một hệ quy chiếu (có hệ tọa độ và mốc thời gian), thì để xác định vận tốc của chuyển động ta tìm:
+ Vận tốc trung bình: \(v_{TB}=\dfrac{\Delta x}{\Delta t}\)
+ Để xác định vận tốc tức thời tại một vị trí, ví dụ tại M ở hình vẽ trên thì ta phải cho N tiến sát đến M, hay \(\Delta t \rightarrow 0\)
Từ đó suy ra: \(v=\lim\limits_{\Delta t\rightarrow0}\dfrac{\Delta x}{\Delta t}\), theo khái niệm đạo hàm ta có giá trị này bằng đạo hàm bậc nhất của tọa độ \(x\) theo thời gian \(t\), viết lại là:
\(v=x'_{(t)}\)
Tương tự ta có gia tốc của chuyển động: \(a=v'_{(t)}\)
Ví dụ: Xét một chuyển động thẳng biến đổi đều có phương trình là:
\(x=10+3.t+2t^2\) (m)
Suy ra phương trình vận tốc là: \(v=x'_{(t)}=3+6.t (m/s)\)
Gia tốc của chuyển động là: \(a=v'_{(t)}=6(m/s^2)\)
Vậy nhé, còn các đại lượng khác thì bạn tìm hiểu trong sách Giải tích 12 sẽ rõ.
VT
13 tháng 1 2017
Giải thích: Đáp án C
Phương pháp: Sử dụng kiến thức về tổng hợp 2 dao động điều hòa
Cách giải:
Theo đề bài ta có PT dao động của hai chất điểm M và N là: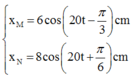 
=> Độ lệch pha giữa hai dao động là π/2 (rad)
Ta biểu diễn hai dao động này bằng véc tơ quay:
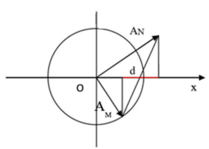
Hai dao động có cùng tần số nên hai véc tơ sẽ quay với cùng tốc độ góc (nghĩa là tam giác OAMAN sẽ không bị biến dạng trong quá trình quay).
Khoảng cách ban đầu giữa M và N là d (như hình vẽ)
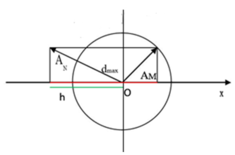
→Khoảng cách giữa M và N lớn nhất hai véc tơ quay đến vị trí để cạnh huyền AMAN song song với Ox
(như hình vẽ)
Khi đó thì chất điểm N cách gốc tọa độ đoạn h (như hình vẽ)
Dựa vào hệ thức lượng trong tam giác vuông ta có:
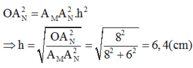
Đáp án B