Tìm phần nguyên của nghiệm lớn nhất trong khoảng − 5 π ; − 2 π của phương trình tan 2 x + 1 tan 3 x − 1 = 1 .
A. − 2 π
B. − 3 π
C. ‒6
D. ‒7
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Đáp án A
Điều kiện x ∈ ℝ
Đặt t = 2 sin x . Phương trình đã cho trở thành t 2 + 2 t = m ( * )
Vì sin x = sin α ⇔ x = α + 2 k π x = π − α + k 2 π nên để phương trình đã cho có tổng các nghiệm trong khoảng 0 ; π bằng π thì phương trình (*) phải có đúng một nghiệm t ∈ 1 ; 2 sin x ∈ 0 ; 1 thì 2 sin x ∈ 1 ; 2
Xét hàm số f t = t 2 + 2 t có bảng biến thiên
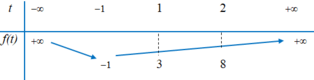
Suy ra để phương trình (*) có đúng một nghiệm t ∈ 1 ; 2 thì m ∈ 3 ; 8 .Vậy tổng các giá trị nguyên của m thỏa mãn yêu cầu bài toán là 4 + 5 + 6 + 7 = 22

Đáp án C
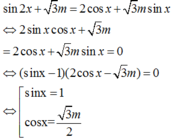
Để phương trình có một nghiệm duy nhất thuộc 0 ; π thì
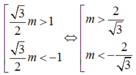

Đáp án A
Ta có c o s x + sin 2 x = 0 ⇔ cos x + 2 sin x cos x = 0 ⇔ [ cos x = 0 sin x = - 1 2 ⇔ [ x = π 2 + k π x = - π 6 + k 2 π x = 7 π 6 + k 2 π
Mà x ∈ - π ; π ⇒ x ∈ - π 2 ; π 2 ; - π 6 ; - 5 π 6 .
Đáp án D.
Điều kiện cos 2 x + 1 ≠ 0 cos 3 x − 1 ≠ 0 . Khi đó:
tan 2 x + 1 tan 3 x − 1 = 1 ⇔ sin 2 x + 1 . sin 3 x − 1 = cos 2 x + 1 . cos 3 x − 1
⇔ cos 3 x − 1 + 2 x + 1 = 0 ⇔ cos 5 x = 0 ⇔ 5 x = π 2 + k π ⇔ x = π 10 + k π 5 , k ∈ ℤ
Mà ta tìm nghiệm lớn nhất nằm trong khoảng − 5 π ; − 2 π ⇒ x = − 21 π 10 ⇒ x = − 7 .