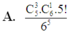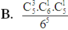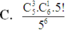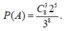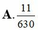Có 5 học sinh không quen biết nhau cùng đến một cửa hàng kem có 6 quầy phục vụ. Xác suất để có 3 học sinh cùng vào 1 quầy và 2 học sinh còn lại vào 1 quầy khác là
A. C 5 3 C 6 1 5 ! 5 6
B. C 5 3 C 6 1 C 5 1 6 5
C. C 5 3 C 6 1 C 5 1 5 6
D. C 5 3 C 6 1 5 ! 6 5