Cho hình chóp .S ABCD có đáy ABCD là hình bình hành thỏa mãn 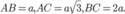 Biết tam giác SBC cân tại S, tam giác SCD vuông tại C và khoảng cách từ D đến mặt phẳng bằng
Biết tam giác SBC cân tại S, tam giác SCD vuông tại C và khoảng cách từ D đến mặt phẳng bằng 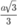 . Tính thể tích V của khối chóp đã cho
. Tính thể tích V của khối chóp đã cho
A. 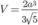
B. 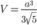
C. 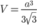
D.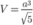
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Đáp án C
![]()
![]()
![]()
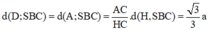
⇔ d ( H ; S B C ) = H K
1 S H 2 + 1 H M 2 = 1 H K 2
⇒ S H = 2 15 a

Chọn A.
Ta chọn (SBC) làm mặt đáy => chiều cao khối chóp là
![]()
Tam giác SBC vuông cân tại S nên
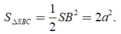
Vậy thể tích khối chóp
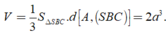

Đáp án D.
Gọi H là trung điểm của AB thì S H ⊥ A B C D ⇒ S H = a 2 .
Khoảng cách từ H đến BC, CD, DA đều là a 2 3 ⇒ S A B C D = 1 2 . a 2 3 . 9 a − a = 2 a 2 3 .
Vậy thể tích khối chóp S.ABCD là V S . A B C D = 1 3 S H . S A B C D = 1 3 . a 2 . 2 a 2 3 = a 3 3 9 .
Đáp án A
Do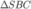 cân tại S nên
cân tại S nên 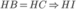 là trung trực của BC.
là trung trực của BC.