Cho hình chóp S.ABCD có đáy là hình vuông ABCD tâm O có cạnh AB = a đường cao SO vuông góc với mặt đáy và SO = a. Khoảng cách giữa SC và AB là:
A . 2 a 5 7
B . a 5 7
C . a 5 5
D . 2 a 5 5
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
CM
21 tháng 5 2019
Đáp án D
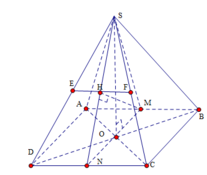
Vì A B / / S C D ⇒ khoảng cách d giữa AB bằng khoảng cách giữa AB và (SCD)
Gọi M,N lần lượt là trung điểm của AB,CD khi đó A B ⊥ S M N
Kẻ đường cao MH của Δ S M N ⇒ M H là khoảng cách giữa AB và SC
Ta có: S N = S O 2 + O N 2 = a 2 + a 2 4 = a 5 2 ⇒ d = M H = S O . M N S N = a . a a 5 2 = 2 a 5 5
CM
14 tháng 3 2017
Đáp án C
Ta có AB// (SCD)
Kẻ O M ⊥ C D tại M, O K ⊥ S M tại K dễ có được O K ⊥ ( S C D )
Ta có:
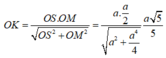
Vậy, d ( A B ; S C ) = 2 a 5 5
Đáp án D
Vì AB//(SCD) => khoảng cách d giữa AB bằng khoảng cách giữa AB và (SCD)
Gọi M, N lần lượt là trung điểm của AB, CD khi đó AB ⊥ (SMN)
Kẻ đường cao MH của ∆ SMN => MH là khoảng cách giữa AB và SC
Ta có: