Một khối chóp tam giác có độ dài các cạnh đáy lần lượt là 6,8,10. Một cạnh bên có độ dài bằng 4 và tạo với đáy một góc 60 0 .Tính thể tích khối chóp
A. 16 3
B. 8 3
C. 16 2 3
D. 16 π
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
CM
Cao Minh Tâm
3 tháng 6 2017
Đúng(0)
Những câu hỏi liên quan
CM
12 tháng 2 2018
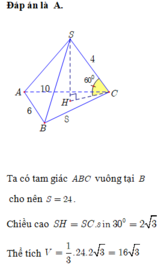
Đáp án là A.
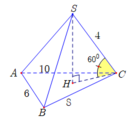
Ta có tam giác ABC vuông tại B cho nên S=24. Chiều cao SH=SC. sin 30 0
Thể tích V= 1 3 . 24 . 2 . 2 3 = 16 3
CM
11 tháng 3 2019
Đáp án là B
Ta có:
• S A B C = 6 2 3 4 = 9 3 c m 2 ; S H = S A . sin 60 0 = 3 3 2 ( c m )
• S S A B = 1 3 .9 3 . 3 3 2 = 27 2 c m 3
CM
3 tháng 8 2019
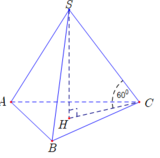
Chọn đáp án C
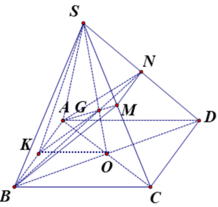
Do S. ABCD đều, có trọng tâm G của tam giác SAC cũng là trọng tâm của SBD.
Nên M, N lần lượt là trung điểm của SC, SD.
Do đó
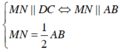
Gọi K là trung điểm của AB, O = AC ∩ BD do S. ABCD đều nên SO ⊥ (ABCD)
ABCD là hình vuông nên có SKO = 60 0
Xét tam giác SKO vuông tại O có KO = a 2 và SKO = 60 0 suy ra:
CM
18 tháng 5 2017
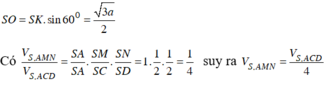
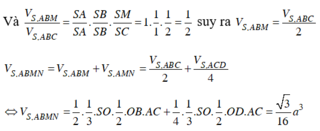
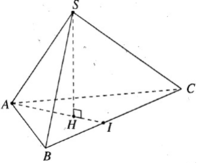
Kẻ SH ⊥ (ABC). Đường thẳng AH cắt BC tại I.
Do S.ABC là hình chóp tam giác đều nên H là trọng tâm của ΔABC.
Do đó
Thể tích khối chóp S.ABC là:
CM
4 tháng 12 2018
Đáp án A
Gọi H là hình chiếu của S lên lên (ABCD).
A H = 2 3 a 2 - a 2 2 = a 3 3 S H = A H tan 60 ∘ = a 3 3 . 3 = a
Thể tích khối chóp là:
V = 1 3 S A B C · S H = 1 3 · 1 2 a 2 sin 60 ° . a = a 3 . 3 12
