Phần II: Tự luận
Trong mặt phẳng (P), cho tam giác đều ABC cạnh a. Trên tia Ax vuông góc với mặt phẳng (P) lấy điểm S sao cho SA = a. Khoảng cách từ A đến (SBC) bằng:
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Kẻ A H ⊥ B C và A H ⊥ S I . Khi đó A H ⊥ S B C ⇒ d A , S B C = A H
Ta có A I = a 3 2 (do ∆ A B C đều cạnh a)
và
S B A B C = S B A ^ = 60 o ⇒ S A = A B . tan 60 = a 3
Vậy d A S B C = A H = S A . A I S A 2 + A I 2 = a 15 5
Đáp án A

Chọn A
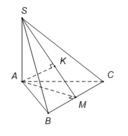
Gọi M là trung điểm BC
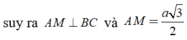
Gọi K là hình chiếu của A trên SM , suy ra AK ⊥ SM. (1)
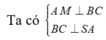
![]()
![]()
![]()
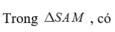
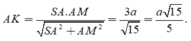
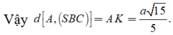

Ta có A I ⊥ B C , S A ⊥ B C
Suy ra V = a 3 , S ∆ A B C = a 2 3 4 ⇒ S A = 4 a 3
Mà A I = a 3 2
Trong tam giác vuông ∆ S A I ta có 1 A K 2 = 1 A S 2 + 1 A I 2 Vậy d = A K = A S 2 . A I 2 A S 2 + A I 2 = 4 a 195 65
Đáp án C

Đáp án B.
Gọi H là trung điểm của BC khi đó S H ⊥ B C do S B C ⊥ A B C ⇒ S H ⊥ A B C
Lại có: C B = 2 C H ⇒ d C ; S A B = 2 d H ; S A B
Dựng H E ⊥ A B H F ⊥ S E ⇒ d H = H F
Mặt khác H E = A C 2 = 1 2 B C . sin A B C ^ = a 4 ; S H = a 3 2
Do đó H F = S H . H E S H 2 + H E 2 = a 39 26 ⇒ d c = a 39 13
● Gọi M là trung điểm của BC ; H là hình chiếu vuông góc của A trên SM.
● Vì tam giác ABC đều nên: BC ⊥ AM.
- Trong tam giác vuông SAM, đường cao AH có: