Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
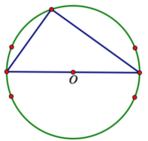
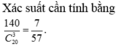
Chọn C
Đa giác đều nội tiếp một đường tròn tâm O. Lấy ngẫu nhiên 3 đỉnh có C 20 3 cách.
Để 3 đỉnh là 3 đỉnh một tam giác vuông không có cạnh nào là cạnh của đa giác đều thực hiện theo các bước:
Lấy một đường kính qua tâm đường tròn có 10 cách ta được 2 đỉnh.
Chọn đỉnh còn lại trong 20 - 2 - 4 = 14 đỉnh (loại đi 2 đỉnh thuộc đường kính và 4 đỉnh gần ngay đường kính đó) cách.
Vậy có tất cả 10.14 = 140 tam giác thoả mãn.
Xác suất cần tính bằng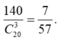 
Chọn C.
Chọn ngẫu nhiên 3 đỉnh của đa giác có: C 20 3 = 1140 cách chọn.
Đa giác đều có 20 đỉnh có 10 đường chéo đi qua tâm đa giác mà cứ 2 đường chéo tại thành 1 hình chữ nhật và 1 hình chữ nhật tạo thành 4 tam giác vuông.
Trong 10 đường chéo đi qua tâm ta trừ đi 10 hình chữ nhật chứa cạnh của (P)
Do đó số tam giác vuông không có cạnh nào của (P) là: 4 C 10 2 - 10 = 140 tam giác.
Vậy xác suất cần tìm là: P = 140/1140 = 7/57
SỐ tam giác tạo được từ 3 đỉnh là \(C^3_{12}\)
Số tam giác có 3 đỉnh là 3 đỉnh của đa giác và 2 cạnh là cạnh của đa giác: cứ 3 đỉnh liên tiếp cho 1 tam giác thỏa mãn
=>Có 12 tam giác
Số tam giác có 3 đỉnh là đỉnh của đa giác và 1 cạnh là cạnh của đa giác
=>CÓ 8*12=96 tam giác
=>\(P=\dfrac{C^3_{12}-12-12\cdot8}{C^3_{12}}\)
Đáp án C
Để các tam giác đó là các tam giác vuông thì cạnh huyền của tam giác đó phải là đường kính của đường tròn.
Với mỗi đường kính của đường tròn (giả sử là AB), có thể nối với 16 đỉnh để tạo thành các tam giác vuông không cân (không nối với C và D) (hình vẽ).
Mà có tất cả 10 đường kính, như vậy số tam giác thỏa mãn đề bài là: 10*16=160.
Xác suất cần tính là 160 C 20 3 = 8 57 .
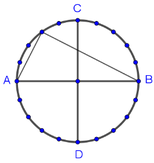
Đáp án C
Chọn ngẫu nhiên 3 đỉnh trong 20 đỉnh có C 20 3 cách n Ω = C 20 3 = 1140
Gọi X là biến cố “3 đỉnh đó là 3 đỉnh của một tam giác vuông không cân”
Đa giác đều 20 đỉnh có 10 đường chéo xuyên tâm, mà cứ 2 đường chéo được 1 hình chữ nhật và 1 hình chữ nhật được 4 tam giác vuông ⇒ số tam giác vuông chọn từ 3 đỉnh trong số 20 đỉnh là 4 . C 10 2 = 180
Tuy nhiên chỉ có 180 - 20 = 160 tam giác vuông không cân n(X) = 160
Vậy P = n X n Ω = 160 1140 = 8 57 .
Đáp án C
Chọn ngẫu nhiên 3 đỉnh trong 20 đỉnh có C 20 3 cách
Gọi X là biến cố “3 đỉnh đó là 3 đỉnh của một tam giác vuông không cân”
Đa giác đều 20 đỉnh có 10 đường chéo xuyên tâm
mà cứ 2 đường chéo được 1 hình chữ nhật và 1 hình chữ nhật được 4 tam giác vuông
⇒ số tam giác vuông chọn từ 3 đỉnh trong số 20 đỉnh là
4 . C 10 2 = 180
Tuy nhiên chỉ có 180 - 20 = 160
tam giác vuông không cân n(X) = 160
Vậy P = n ( X ) n ( Ω ) = 8 57
Đáp án C
Chọn ngẫu nhiên 3 đỉnh trong 20 đỉnh có C 20 3 cách ⇒ n Ω = 1140
Gọi X là biến cố “3 đỉnh đó là 3 đỉnh của một tam giác vuông không cân”
Đa giác đều 20 đỉnh có 10 đường chéo đi qua tâm đa giác mà cứ 2 đường chéo tạo thành 1 hình chữ nhật và 1 hình chữ nhật tạo thành 4 tam giác vuông số tam giác vuông là 4. C 10 2 = 180
Tuy nhiên, trong C 10 2 hình chữ nhật có 5 hình vuông nên số tam giác vuông cân là 5.4 = 20
Do đó, số kết quả thuận lợi cho biến cố X là n X = 180 − 20 = 160 . Vậy P = n X n Ω = 8 57
