Với giá trị nào của m để phương trình m sin 2 x -3sinx.cosx-m-1=0 có đúng nghiệm x ∈ 0 ; 3 π 2 ?
A. m ≤ -1
B.m < -1
C. m ≥ -1
D. m>-1
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
CM
7 tháng 3 2019
Đáp án B
Cách 1: Tự luận thuần túy.
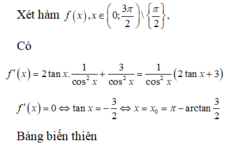
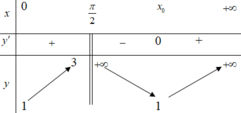
Từ BBT ta thấy, để phương trình có 3 nghiệm phân biệt trong khoảng
Cách 2 (casio):
Thử bằng MTCT, sử dụng Mode 7
+ Thử với m= -2 ta thấy f(x) đổi dấu 3 lần nên có 3 nghiệm (loại đáp án C,D)
+ Thử với m = -1 ta thấy f(x) đổi dấu 2 lần nên có 2 nghiệm (loại A).
CM
30 tháng 1 2017
Đáp án C
PT đã cho
⇔ m sin 2 x − 1 − 3 sin x cos x − 1 = 0 ⇔ 3 sin x cos x + cos 2 x + 1 = 0
Dễ thấy cos x ≠ 0 ⇒ P T ⇔ tan 2 x + 3 tan x + m + 1 = 0
Để PT đã cho có ba nghiệm thuộc 0 ; 3 π 2 thì PT t 2 + 3 t + m + 1 = 0 có hai nghiệm trái dấu ⇔ m + 1 < 0 ⇔ m < − 1
CM
2 tháng 10 2017
Đáp án B.
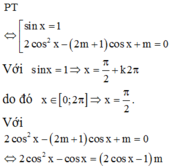
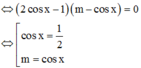
PT: cos x = 1 2 có 2 nghiệm thuộc trên đoạn 0 ; 2 π do đó để PT đã cho có 4 nghiệm thực thuộc đoạn 0 ; 2 π thì
TH1: m= cosx có 1 nghiệm thuộc đoạn 0 ; 2 π
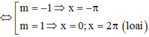
TH2: m= cosx có 2 nghiệm thuộc đoạn 0 ; 2 π trong đó có 1 nghiệm trùng
Vậy m= -1; m=0.
NV
Nguyễn Việt Lâm
Giáo viên
22 tháng 12 2020
\(\Leftrightarrow1-2sin^2x+\left(2m-3\right)sinx+m-2=0\)
\(\Leftrightarrow2sin^2x-\left(2m-3\right)sinx-m+1=0\)
\(\Leftrightarrow2sin^2x+sinx-2\left(m-1\right)sinx-\left(m-1\right)=0\)
\(\Leftrightarrow sinx\left(2sinx+1\right)-\left(m-1\right)\left(2sinx+1\right)=0\)
\(\Leftrightarrow\left(2sinx+1\right)\left(sinx-m+1\right)=0\)
\(\Leftrightarrow\left[{}\begin{matrix}sinx=-\dfrac{1}{2}\\sinx=m-1\end{matrix}\right.\)
Pt có đúng 2 nghiệm thuộc khoảng đã cho khi và chỉ khi:
\(\left\{{}\begin{matrix}m-1\ne-\dfrac{1}{2}\\-1\le m-1\le1\end{matrix}\right.\) \(\Leftrightarrow\left\{{}\begin{matrix}m\ne\dfrac{1}{2}\\0\le m\le2\end{matrix}\right.\)
NV
Nguyễn Việt Lâm
Giáo viên
21 tháng 3 2022
- Với \(m=-1\Rightarrow4< 0\) không thỏa mãn
- Với \(m\ne-1\) BPT nghiệm đúng với mọi x khi và chỉ khi:
\(\left\{{}\begin{matrix}m+1< 0\\\Delta'=\left(m+1\right)^2-4\left(m+1\right)< 0\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}m< -1\\\left(m+1\right)\left(m-3\right)< 0\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}m< -1\\-1< m< 3\end{matrix}\right.\)
\(\Rightarrow\) Không tồn tại m thỏa mãn yêu cầu
CM
14 tháng 3 2017
Đáp án C
Sử dụng tính đơn điệu của hàm số, đánh giá số nghiệm của phương trình.
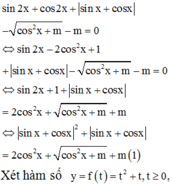
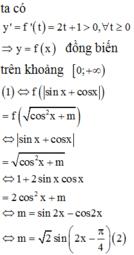
Vậy, có 3 giá trị nguyên của m thỏa mãn yêu cầu đề bài.
Đáp án B
Bảng biến thiên
Từ BBt ta thấy, để phương trình có 3 nghiệm phân biệt trong khoảng
Cách 2 (casio): Thử bằng MTCT, sử dụng Mode 7
+ Thử với m = -2 ta thấy f(x) đổi dấu 3 lần nên có 3 nghiệm (loại đáp án C,D)
+ Thử với m = -1 ta thấy f(x) đổi dấu 2 lần nên có 2 nghiệm (loại A).