Cho tứ diện ABCD có AD ⊥ (ABC), ABC là tam giác vuông tại B. Biết
BC=A, AB=a 3 , AD=3a Quay các tam giác ABC và ABD xung quanh đường thẳng AB ta được 2 khối tròn xoay. Thể tích phần chung của 2 khối tròn xoay đó bằng
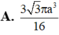
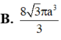
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Đáp án A
Vì hai mặt phẳng (ABC), (ABD) vuông góc với nhau nên bài toán trở thành “Tính thể tích khối tròn xoay khi quay tam giác HAB quanh AB với ABCD là hình thang vuông tại A,B” như hình bên. Hai tam giác BHC và DHA đồng dạng ⇒ B H D H = H C H A = B C A D = 1 3 .
Mà B D = A D 2 + A B 2 = 2 a 3 ; A C = A B 2 + C B 2 = 2 a
Suy ra A H = 3 4 A C = 3 4 .2 a = 3 a 2 và B H = 1 4 B D = 1 4 .2 a 3 = a 3 2 .
Diện tích tam giác ABH là:
S Δ A B H = 1 2 . A H . B H = 1 2 . 3 a 2 . a 3 2 = 3 a 2 3 8 = 1 2 . d H ; B C . B C ⇒ d H ; B C = 2. 3 a 2 3 8 . a 3 = 3 a 4 .
Vậy thể tích khối tròn xoay cần tính là:
V = 1 3 π 3 a 4 2 . a 3 = 3 3 π a 2 16 .

Đáp án A
Khi quay hình tam giác đó xung quanh đường thẳng AB một góc 3600 ta được một khối nón tròn xoay có đỉnh A, đường cao AB, bán kính đáy R = BC.
Kết luận V = 1 3 . π . BC 2 . AB = πa 3

Đáp án C
Khi quay tam giác theo BC ta sẽ có được hai khối nón như hình vẽ.
Trong ΔABC, gọi H là chân đường cao của A đến BC. Ta có

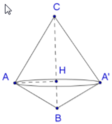

Khi quay tam giác theo BC ta sẽ có được hai khối nón như hình vẽ.
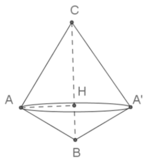
Trong △ A B C , gọi là H chân đường cao của A đến BC. Ta có:
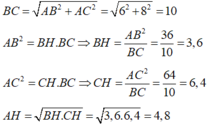
Thể tích hình nón đỉnh C là:
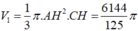
Thể tích hình nón đỉnh B là:
![]()
Khối tròn xoay có thể tích:
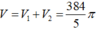

Đáp án C
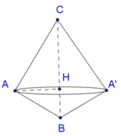
Khi quay tam giác theo BC ta sẽ có được hai khối nón như hình vẽ.
Trong ∆ A B C , gọi là H chân đường cao của A đến BC. Ta có
