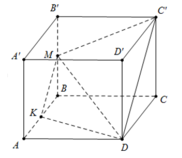
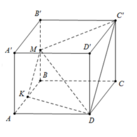
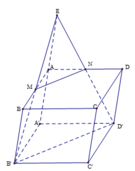
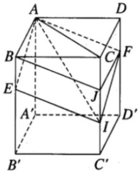
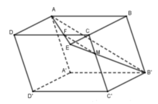
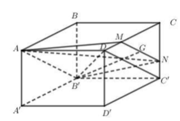
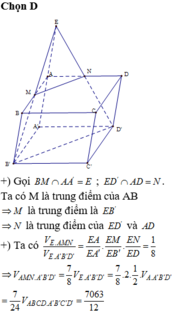
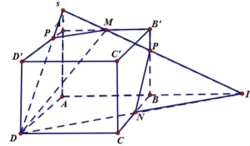
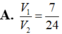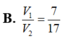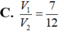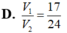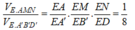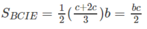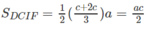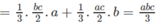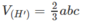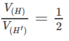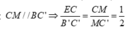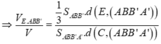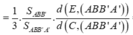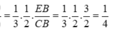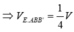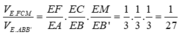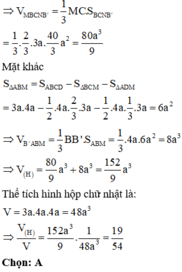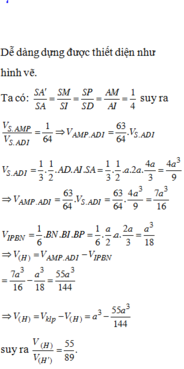Cho khối hộp chữ nhật ABCD.A'B'C'D'. Gọi M là trung điểm của BB'. Mặt phẳng (MDC') chia khối hộp chữ nhật thành hai khối đa diện, một khối chứa đỉnh C và một khối chứa đỉnh A'. Gọi V 1 , V 2 lần lượt là thể tích hai khối đa diện chứa C và A'. Tính V 1 V 2 .