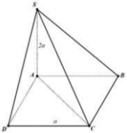
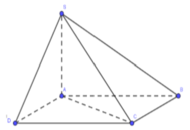
Cho hình chóp S.ABCD có đáy ABCD là hình chữ nhật với AB=a, AD=2a, SA=2a và SA ⊥ (ABCD), Gọi a là góc giữa 2 đường thẳng SC và BD. Khi đó, cos α bằng
![]()
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


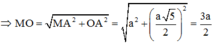
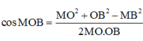
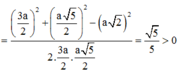
![]()
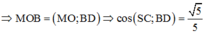

Đáp án C
Phương pháp:
- Xác định góc giữa hai đường thẳng: Cho a, b là hai đường thẳng bất kì, đường thẳng a’ // a => (a;b) = (a’;b)
Cách giải:

Gọi O, M lần lượt là tâm của hình chữ nhật ABCD và trung điểm của SA
=> MO là đường trung bình của tam giác SAC
=>MO//SC
=>(BD,SC)=(BD,MO)
+) ABCD là hình chữ nhật
![]()
![]()
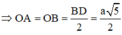
+) M là trung điểm SA
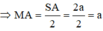
Tam giác MAB vuông tại A
![]()
Tam giác MAO vuông tại A
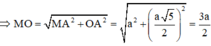
+) Xét tam giác MBO:
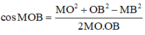

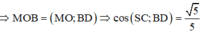

Chọn C.
Phương pháp:
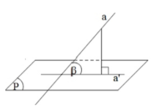
Gọi a’ là hình chiếu vuông góc của a trên mặt phẳng (P).
Góc giữa đường thẳng a và mặt phẳng (P) là góc giữa đường thẳng a và a’.
Cách giải:
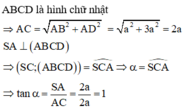

Đáp án D
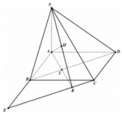
Dựng ![]()
Dựng ![]()
Khi đó Cx cắt AB tại E và AK tại I suy ra BI là đường trung bình của ∆AEK ( Do BD qua trung điểm O của AC)
Ta có: 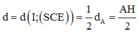
Do 
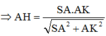
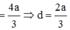

Đáp án A.
Phương pháp
Góc giữa đường thẳng và mặt phẳng là góc giữa đường thẳng và hình chiếu của nó trên mặt phẳng đáy.
Cách giải
S C ; A B C D = S C ; A C = S C A
ABCD là hình vuông cạnh a ⇒ A C = a 2
Xét tam giác vuông SAC có:
tan = S A A C = 2 a a 2 = 2