Cho hình chóp S.ABCD có đáy là hình vuông cạnh 2a, tam giác SAB đều, góc giữa (SCD) và (ABCD) bằng 60 0 . Gọi M là trung điểm của cạnh AB. Biết hình chiếu vuông góc của đỉnh S trên mặt phẳng (ABCD) nằm trong hình vuông ABCD. Tính theo a khoảng cách giữa hai đường thẳng SM và AC.
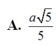
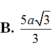
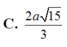
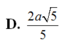





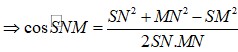
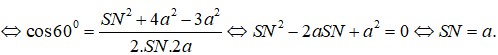

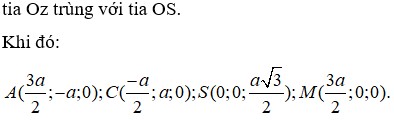
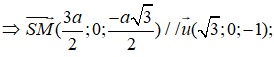
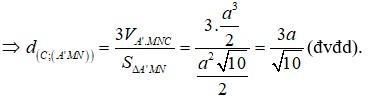

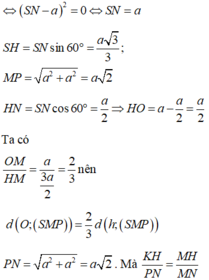
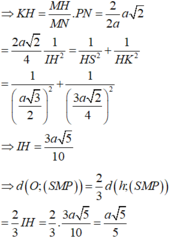
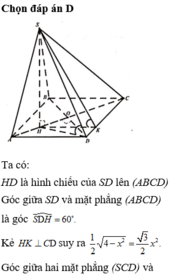

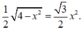


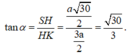
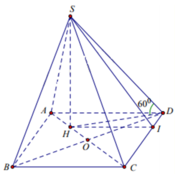

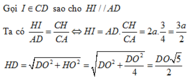
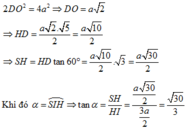
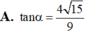
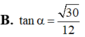
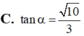
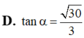

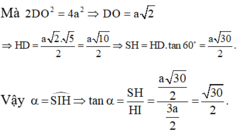
Đáp án A