Hình nón có thiết diện qua trục là một tam giác đều cạnh 2a, diện tích toàn phần là S 1 và mặt cầu có đường kính bằng chiều cao hình nón, có diện tích S 2 . Khẳng định nào sau đây đúng?
![]()
![]()
![]()
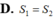
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

![]()



Đáp án A
Hình nón có thiết diện qua trục là Δ đều cạnh 4
=> Bán kính đáy r=2 độ dài đường sinh l=4.
Suy ra diện tích toàn phần của hình nón là: S t p = π r l + π r 2 = π .2.4 + π .2 2 = 12 π .
Vậy bán kính mặt cầu là: S = 4 π R 2 ⇒ R = S 4 π = 12 π 4 π = 3

Chọn D.
(h.2.60) Bán kính đáy của hình nón là a, đường sinh của hình nón là 2a.
Do đó, ta có:
S 1 = π Rl = π .a.2a = 2 πa 2 (1)
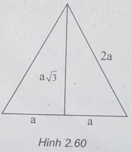
Mặt cầu có bán kính là a 3 /2, nên ta có:
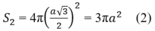
Từ (1) và (2) suy ra: 2 S 2 = 3 S 1

Chọn D.
Hình nón có bán kính đáy là a, chiều cao a 3 nên có thể tích:
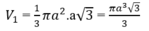
Hình cầu có bán kính (a
3
)/2 nên có thể tích:![]()
Từ đó suy ra: 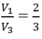

Đáp án A
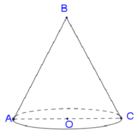
Thiết diện là tam giác vuông cân tại đình B, cạnh huyền AC = 2.
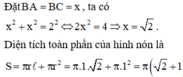

Đáp án D
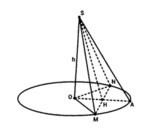
Thiết diện là tam giác SMN cân tại S.
Kẻ bán kính OA của hình nón
vuông góc với MN tại H

