Tính diện tích hình phẳng giới hạn bởi parabol y = x 2 - 2 x và đường thẳng y = x
A. 9/2
B. 11/6
C. 27/6
D. 17/6
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Chọn B.
Phương pháp: Tìm hoành độ giao điểm và lấy tích phân để tích diện tích.
Cách giải: Phương trình hoành độ giao điểm là:
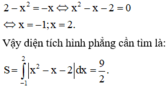

Miền cần tính diện tích được thể hiện bởi Hình 9 (học sinh tự làm)
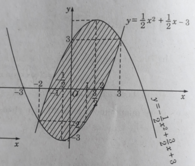
Như vậy, với mọi x ∈ (-2;3) đồ thị của hàm số
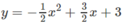
nằm phía trên đồ thị của hàm số
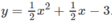
Vậy ta có:
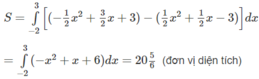

a) Phương trình hoành độ giao điểm f(x) = X2 - x - 2 =0 ⇔ x = -1 hoặc x = 2.
Diện tích hình phẳng cần tìm là :
b) Phương trình hoành độ giao điểm:
f(x) = 1 - ln|x| = 0 ⇔ lnx = ± 1
⇔ x = e hoặc
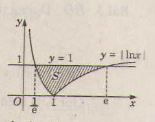
y = ln|x| = lnx nếu lnx ≥ 0 tức là x ≥ 1.
hoặc y = ln|x| = - lnx nếu x < 0, tức là 0 < x < 1.
Dựa vào đồ thị hàm số vẽ ở hình trên ta có diện tích cần tìm là :
Ta có ∫lnxdx = xlnx - ∫dx = xlnx – x + C, thay vào trên ta được :
c) Phương trình hoành độ giao điểm là:
f(x) = 6x – x2 – (x - 6)2 = -2(x2 – 9x +18)
f(x) = 0 ⇔ -2(x2 – 9x +18) ⇔ x = 3 hoặc x = 6.
Diện tích cần tìm là:
Hoành độ giao điểm của (P) và (d) là nghiệm phương trình:
Đáp án A