Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Chọn đáp án C
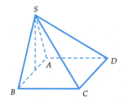
Ta có mặt cầu ngoại tiếp hình chóp S.ABCD chính là mặt cầu ngoại tiếp hình chóp S.ABC.
Đáp án A
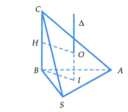
Gọi N là trung điểm của MD, khi đó N là tâm đường tròn ngoại tiếp tam giác vuông ADM.
Dựng đường thẳng Δ đi qua N và song song với SA⇒Δ là trục đường tròn ngoại tiếp tam giác ADM.
Dựng mặt phẳng trung trực (P) của SA, P ∩ Δ = I , khi đó I là tâm của mặt cầu ngoại tiếp hình chóp SADM, bán kính R = IA .
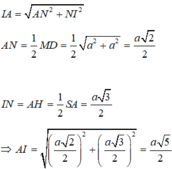
Đáp án A.
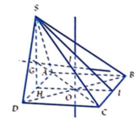
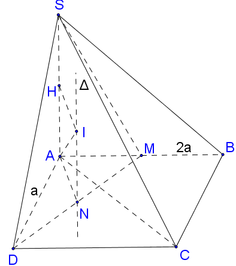
Trong mặt phẳng (ABCD), gọi O = A C ∩ B D , H là trung điểm AD.
Gọi I,J lần lượt là trung điểm của BC và G là trọng tâm Δ S A D .
Đường thẳng d qua O và vuông góc với (ABCD) gọi là trục của đường tròn ngoại tiếp đáy (ABCD).
∆ qua G và vuông góc với (SAD) là trục của đường tròn ngoại tiếp (SAD).
Trong mặt phẳng (SHI), gọi I = ∆ ∩ d
⇒ J cách đều các đỉnh của hình chóp
⇒ J là tâm mặt cầu ngoại tiếp S.ABCD có bán kính
R = J D = O J 2 + O D 2 = G H 2 + O D 2
Có G H = 1 3 S H = 1 3 . a . 3 2 = a 3 6 ;
O D = 1 2 D B = a 5 2 ⇒ R = 3 a 2 56 + 5 a 2 4 = 4 3 a ⇒ S m c = 4 πR 2 = 16 3 a 2
Đáp án A.
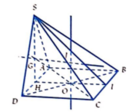
Trong mặt phẳng (ABCD) gọi: 
H là trung điểm AD.
Gọi I,J lần lượt là trung điểm của BC và G là trọng tâm ∆ SAD
Đường thẳng d qua O và vuông góc với (ABCD) gọi là trục của đường tròn ngoại tiếp đáy (ABCd).
∆ qua G và vuông góc với (SAD) là trục của đường tròn ngoại tiếp (SAD).
Trong mặt phẳng (SHI), gọi I = ∆ ∩ d
=> J cách đều các đỉnh của hình chóp
=> J là tâm mặt cầu ngoại tiếp S.ABCD có bán kính
R = JD = 
Có 
