Cho tứ diện ABCD có AB=6a, CD=8a và các cạnh còn lại bằng a 74 . Tính diện tích mặt cầu ngoại tiếp tứ diện ABCD.
![]()
![]()
![]()
![]()
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

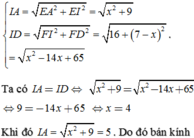
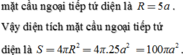

Đán án C
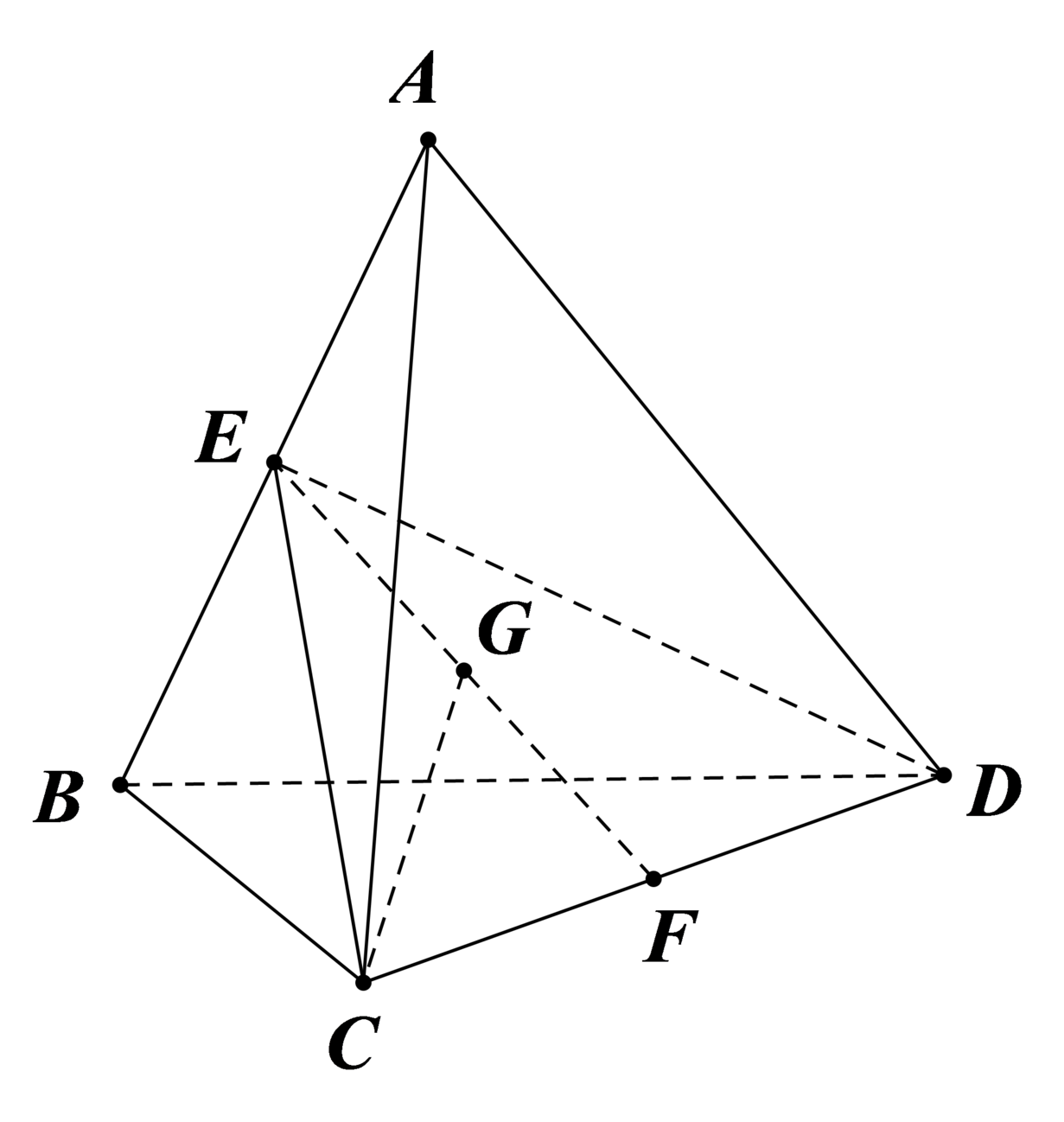
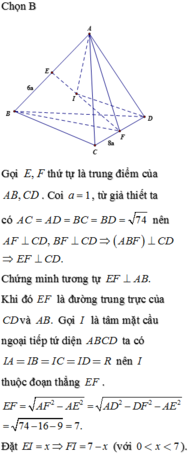
Gọi G là trung điểm của EF thì G chính là tâm mặt cầu ngoại tiếp tứ diện.
Ta có C E 2 = C B 2 + C A 2 2 − A B 2 4 = 6 2 + 6 2 2 − 2 2 4 = 35 ,
E F 2 = C E 2 − C F 2 = 35 − 2 2 = 31
⇒ G F = 31 2 ⇒ R = G C = G F 2 + C F 2 = 31 4 + 4 = 47 2 .
Vậy diện tích mặt cầu cần tính là:
S = 4 π R 2 = 4 π . 47 4 = 47 π .

Hóng ké ai đó giải bài nì, ko thì toi xách mông đi hỏi, ngu hình quá :(

Ta có O là tâm của hình hộp chữ nhật AC'BD'.A'C'B'D nên nó là tâm của mặt cầu ngoại tiếp tứ diện ABCD. Bán kính của mặt cầu ngoại tiếp tứ diện ABCD là
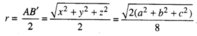
Gọi H và K theo thứ tự là chân đường vuông góc kẻ từ O đến (ABC) và (ABD). Vì OA = OB = OC nên HA = HB = HC, tương tự KA = KB = KD. Vì ΔABD = ΔBAC nên HA = KA. Do đó OH = OK. Tương tự, ta chứng minh được khoảng cách từ O đến các mặt của tứ diện ABCD bằng nhau nên O cũng là tâm của mặt cầu nội tiếp tứ diện ABCD.
Khi đó ta có V ABCD = V OABC + V OBCD + V OCDA + V ODAB
= 4 V OABC = 4 r ' S ABC / 3
Do đó:
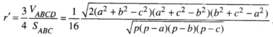
Trong đó 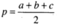

Chọn A
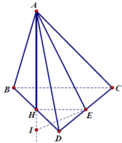
Coi như a = 1 . Tam giác ACD vuông tại A nên A D = C D 2 - A C 2 = 1 = A B cân tại A và tam giác ACD vuông cân tại A. Gọi H, E lần lượt là trung điểm của BD và DC. Ta có A H ⊥ B C D và C D ⊥ A E . Hơn nữa C D ⊥ A H ⇒ C D ⊥ A H E ⇒ C D ⊥ H E mà HE song song với BC suy ra BC vuông góc với CD. H là tâm của đường tròn ngoại tiếp tam giác BCD, do đó AH là trục đường tròn này. Trong tam giác AHE dựng đường thẳng qua E vuông góc AE và cắt AH tại điểm I. Do mặt phẳng (AHE) vuông góc với mặt phẳng (ACD) nên d cũng vuông góc với (ACD). Hơn nửa E là tâm của đường tròn ngoại tiếp tam giác ACD suy ra I là tâm của mặt cầu ngoại tiếp tứ diện ABCD.
Ta có A I . A H = A E 2 ⇒ A I = A E 2 A H . Ta có A E = 1 2 C D = 2 2 , H K = 1 2 B C = 1 2 ⇒ A H = 1 2
Vậy A I = A E 2 A H = 1 ⇒ R = 1 ⇒ V m c = 4 3 πa 3