Ông A vay ngân hàng 200 triệu đồng với lãi suất 1%/tháng. Ông ta muốn hoàn nợ cho ngân hàng theo cách sau: Sau đúng một tháng kể từ ngày vay, ông bắt đầu hoàn nợ; hai lần hoàn nợ liên tiếp cách nhau đúng một tháng, số tiền hoàn nợ ở mỗi tháng là như nhau. Biết rằng mỗi tháng ngân hàng chỉ tính lãi trên số dư nợ thực tế của tháng đó và sau đúng hai năm kể từ ngày vay ông A trả hết nợ. Hỏi số tiền mỗi tháng ông ta cần trả cho ngân hàng gần nhất với số tiền nào dưới đây?
A. 9,85 triệu đồng
B. 9,44 triệu đồng
C. 9,5 triệu đồng
D. 9,41 triệu đồng






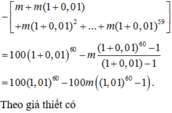
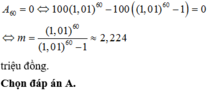
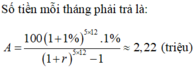
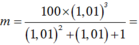
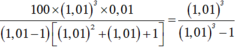
Chọn D