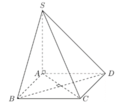
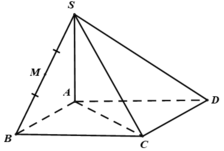
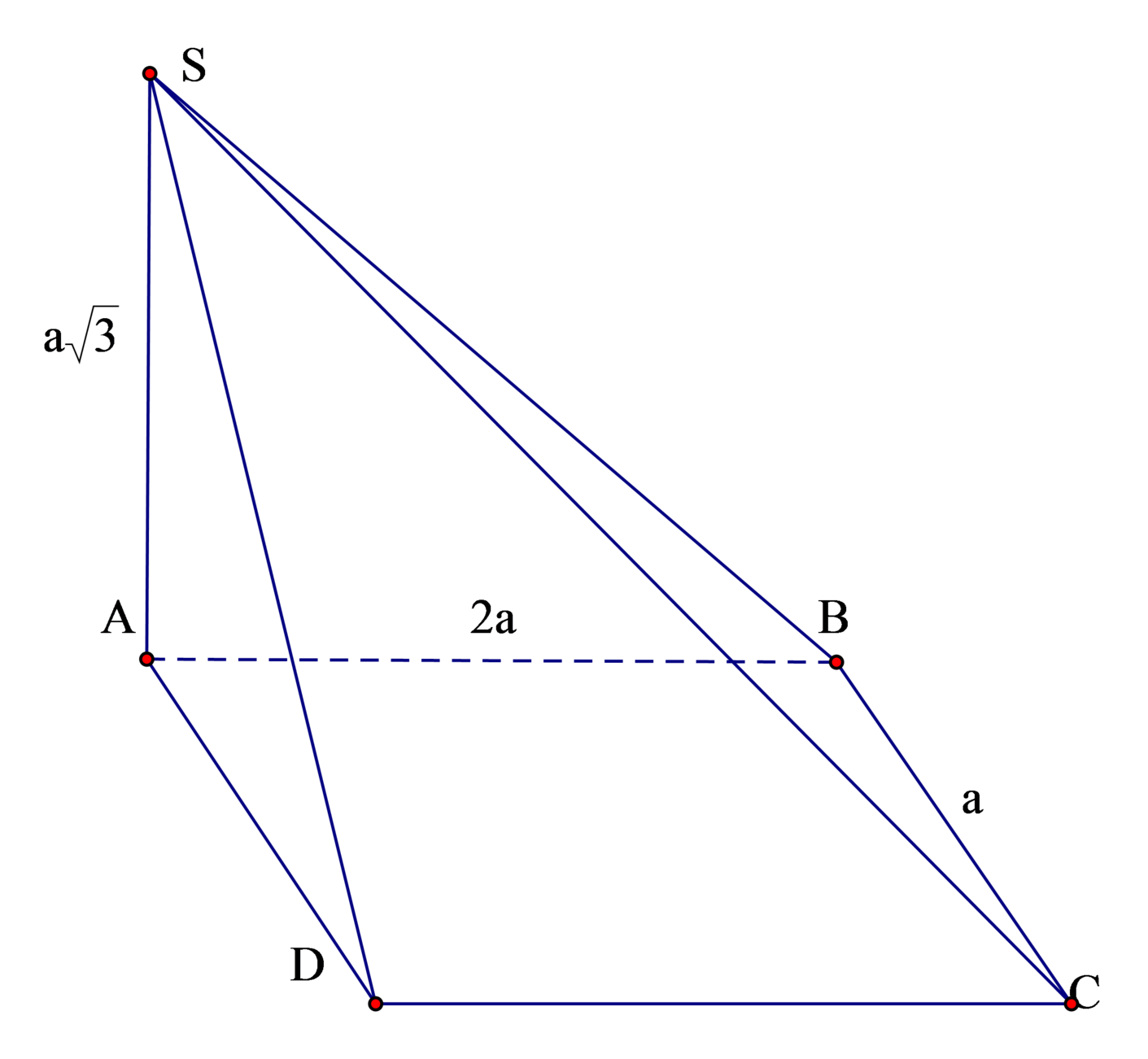
Cho hình chóp S.ABCD có đáy ABCD là hình chữ nhật, A B = a , A D = 3 a ; hai mặt phẳng (SAB) và (SAC) cùng vuông góc với mặt phẳng (ABCD); góc giữa hai mặt phẳng (SBC) và (ABCD) bằng 60 0 Khi đó khối chóp S.ABC có thể tích là
A. 3 a 3 3 .
B. 3 a 3 4 .
C. 3 a 3 .

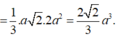


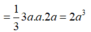

Đáp án B
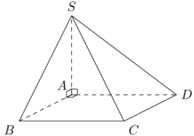
Vì (SAB),(SAC) cùng vuông góc với (ABCD) nên giao tuyến S A ⊥ A B C D
Do AB, SB cùng vuông góc với giao tuyến BC của (ABCD) và (SBC) nên góc giữa hai mặt phẳng trên là góc:
S B A = 60 0 ⇒ S A = A B . sin 60 0 ⇒ S A = a 3 2
Vậy:
V S . A B C = 1 3 S A . A B . B C = 1 3 a 3 2 . a .3 a 2 = a 3 3 4