Cho hàm số y = x + 3 x + 1 C . Đường thẳng d : y = 2 x + m cắt (C) tại 2 điểm phân biệt M, N và MN nhỏ nhất khi
A. m = − 1
B. m = 3
C. m = 2
D. m = 1
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Đáp án A
+ Phương trình hoành độ giao điểm: ![]()
+ Điều kiện để d cắt tại hai điểm phân biệt là ![]() .
.
+ Trung điểm của MN là I.
+ Theo công thức đường trung tuyến 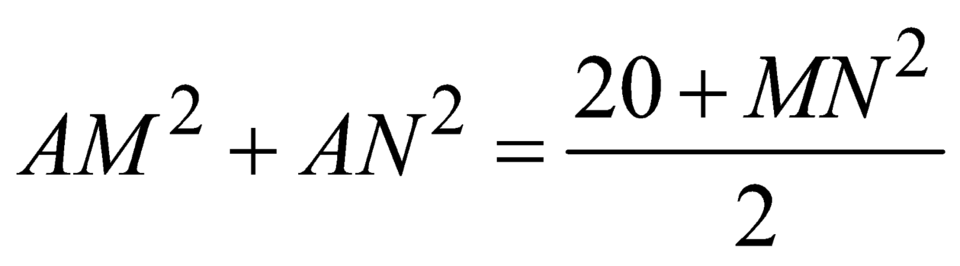 .
.
![]() nhỏ nhất khi
nhỏ nhất khi ![]() nhỏ nhất.
nhỏ nhất.
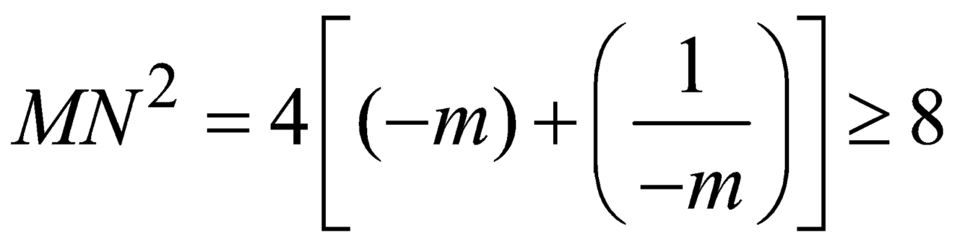 , dấu bằng xảy ra khi
, dấu bằng xảy ra khi ![]()

Lời giải:
Phương trình hoành độ giao điểm:
\(2x+m-\left(x+\frac{3}{x}+1\right)=0\)
\(\Leftrightarrow x^2+x(m-1)-3=0\)
Để hai đths cắt nhau tại hai điểm phân biệt thì pt trên phải có hai nghiệm phân biệt.
\(\Rightarrow \Delta=(m-1)^2+3>0\) (luôn đúng với mọi m)
Khi đó, gọi \(x_1,x_2\) là hai nghiệm của pt thì theo hệ thức Viete:
\(\left\{\begin{matrix} x_1+x_2=1-m\\ x_1x_2=-3\end{matrix}\right.\)
Hai giao điểm là \(M(x_1,2x_1+m); N(x_2,2x_2+m)\)
\(MN=\sqrt{(x_1-x_2)^2+(2x_1+m-2x_2-m)^2}=\sqrt{5(x_1-x_2)^2}\)
Có \((x_1-x_2)^2=(x_1+x_2)^2-4x_1x_2=(m-1)^2+12\geq 12\)
\(\Rightarrow MN\geq \sqrt{60}\) hay \(MN_{\min}=\sqrt{60}\)
Dấu bằng xảy ra khi \(m=1\)

Phương trình hoành độ giao điểm: x 2 − 2 x − 2 = x + m ⇔ x 2 − 3 x − 2 − m = 0
(d) cắt (P) tại hai điểm phân biệt A, B ⇔ Δ > 0 ⇔ 17 + 4 m > 0 ⇔ m > − 17 4
Giả sử (*) có hai nghiệm x 1 , x 2 thì x 1 + x 2 = − b a = 3 x 1 . x 2 = c a = − m − 2
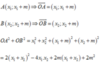
= 18 − 4 ( − 2 − m ) + 6 m + 2 m 2 = 2 m 2 + 10 m + 26 = 2 m + 5 2 2 + 27 2 ≥ 27 2 với m > − 17 4
Vậy giá trị nhỏ nhất của O A 2 + O B 2 là 27 2 khi m = − 5 2
Đáp án cần chọn là: A
Đáp án là B.
+ Phương trình hoành độ giao điểm của hai đồ thị:
2 x 2 + m + 1 x + m − 3 = 0 ; x ≠ − 1 (1)
+ Gọi M x 1 ; 2 x 1 + m ; N x 2 ; 2 x 2 + m , trong đó x 1 ; x 2 là nghiệm phương trình (1)
Ta có: x 1 + x 2 = m + 1 2 ; x 1 . x 2 = m − 3 2 ;
M N = 5 x 1 + x 2 2 − 4 x 1 x 2 = 5 4 m − 3 2 + 16 ≥ 2 5
+ min M N = 2 5 ⇔ m = 3.