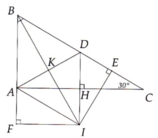
Cho tam giác ABC có hai đỉnh B, C cố định BC = 2a và đỉnh A thay đổi. Qua B dựng đường thẳng d vuông góc với BC, d cắt đường trung tuyến AI của tam giác ABC tại K. Gọi H là trực tâm của tam giác ABC, biết rằng IH song song với KC. Tìm quỹ tích điểm A là
A. Đường thẳng x+2y+4a=0
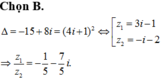
![]()
D. Parabôn y=2ax2