Một chất điểm chuyển động với vận tốc v=30(m/s) thì đột ngột thay đổi gia tốc a(t)= 4-t (m/s2). Tính quãng đường đi được từ thời điểm thay đổi gia tốc đến thời điểm vận tốc nhỏ nhất
A.424/3 (m)
B. 848/3(m)
C. 128/3 (m)
D. 64/3 (m)
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a/ \(v^2-v_o^2=2as\)
\(\Leftrightarrow s=\dfrac{v^2-v_o^2}{2as}=156,25\left(m\right)\)
b/ \(s_1=\dfrac{1}{2}at_1^2=\dfrac{1}{2}.2.4^2=16\left(m\right)\)
\(s_2=\dfrac{1}{2}at_2^2=\dfrac{1}{2}.2.3^2=9\left(m\right)\)
\(s_4=s_1-s_2=16-9=7\left(m\right)\)
c/ \(v=v_o+at\Leftrightarrow t=\dfrac{v-v_o}{a}=12,5\left(s\right)\)
\(s_{t-1}=\dfrac{1}{2}a\left(t-1\right)^2=132,25\left(m\right)\)
\(s_{cuoi}=s-s_{t-1}=24\left(m\right)\)
d/ \(s_{t-2}=\dfrac{1}{2}a\left(t-2\right)^2=110,25\left(m\right)\)
\(s_{2cuoi}=s-s_{t-2}=46\left(m\right)\)

Theo đề bài, ta có:
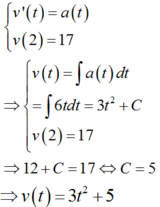
Quãng đường vật đó đi được trong khoảng thời gian tử thời điểm t = 4 giây đến thời điểm t = 10 giây là:
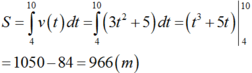
Chọn: D