Cho hình chóp S.ABCD, đáy ABCD là hình bình hành, mặt phẳng α đi qua AB cắt cạnh SC, SD lần lượt tại M, N. Tính tỉ số S N S D để α chia khối chóp S.ABCD thành hai phần có thể tích bằng nhau.
A. 1 2
B. 1 3
C. 5 - 1 2
D. 3 - 1 2
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Chọn C

Ta có: α ∩ ( S C D ) = M N ⇒ M N / / C D .
Do đó α là (ABMN).
Mặt phẳng α chia khối chóp thành 2 phần có thể tích bằng nhau là
V S . A B M N = V A B C D M N ⇒ V S . A B M N = 1 2 . V S . A B C D 1
Ta có:
V S . A B C = V S . A C D = 1 2 V S . A B C D
Đặt S N S D = x với (0<x<1), khi đó theo Ta-let ta có S N S D = S M S C = x .
Mặt khác
V S . A B M V S . A B C = S A S A . S B S B . S M S C = x ⇒ V S . A B M = x 2 V S . A B C D
V S . A M N V S . A C D = S A S A . S M S C . S N S D = x 2 ⇒ V S . A M N = x 2 2 V S . A B C D
⇒ V S . A B M N = V S . A B M + V S . A M N = ( x 2 + x 2 2 ) . V S . A B C D 2
Từ (1), (2) suy ra
x 2 + x 2 2 = 1 2 ⇔ x 2 + x - 1 = 0
x = - 1 - 5 2 v à x = - 1 + 5 2
Đối chiếu điều kiện của x ta được S N S D = - 1 + 5 2

Đáp án D
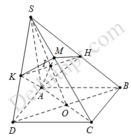
Gọi O là tâm của hình bình hành ABCD, nối S O ∩ A M = I .
Qua I kẻ đường thẳng d, song song với BD cắt SB, SD lần lượt tại H, K suy ra



Đáp án D

Gọi O là tâm của hình bình hành ABCD, nối S O ∩ A M = I
Qua I kẻ đương thẳng d, song song với BD cắt SB, SD lần lượt tại H, K suy ra S H S B = S K S D = S I S O .
Điểm M ∈ S C thỏa mãn 5 S M = 2 S C ⇒ S M S C = 2 5
Xét tam giác SAC, có:
M S M C . A C A O . I O I S = 1 ⇒ I O S I = 4 3 ⇒ S I S O = 3 7
Khi đó:
V S . A K M V S . A D C = S K S D . S M S C ; V S . A H M V S . A B C = S H S B . S M S C
Suy ra:
V S . A H M K V S . A B C D = S M S C . S H S B = 2 5 . 3 7 = 6 35 ⇒ V S . A H M K = 6 36 V S . A B C D

Với x = S A S A = 1 ; y = S M S B , z = S N S C ; t = S P S D
ta có 1 x + 1 z = 1 y + 1 t và xét tam giác SAC ta có
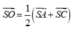
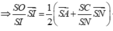
![]()
Mặt khác ba điểm A, I, N thẳng hang nên
1 4 + 1 4 z = 1 ⇔ z = 1 3
Do đó 1 y + 1 t = 1 1 + 1 1 3 = 4 ⇒ y = t 4 t - 1
Vì vậy
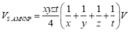
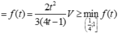
Dấu bằng đạt tại t = 1 2 ; y = 1 2 . Tức mặt phẳng α đi qua trung điểm các cạnh SB. SD.
Chọn đáp án C.

Đáp án A
Phương pháp giải:
Dùng định lí Thalet và phương pháp tỉ số thể tích để tính thể tích khối chóp cần tìm

Đáp án là C