Cho hàm số y = 1 3 x 3 + m 2 x − 2 m 2 + 2 m − 9 , m là tham số. Gọi S là tất cả các giá trị của m sao cho giá trị lớn nhất của hàm số trên đoạn 0 ; 3 không vượt quá 3. Tìm S?.
A. S = − ∞ ; − 3 ∪ 1 ; + ∞
B. S = − 3 ; 1
C. S = − ∞ ; − 3 ∪ 1 ; + ∞
D. S = − 3 ; 1

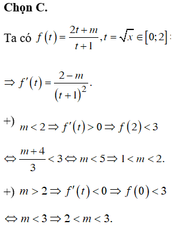
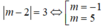
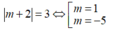

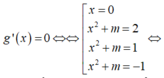





Đáp án B
Ta có: y ' = x 2 + m 2 ≥ 0 ∀ x ∈ 0 ; 3
Do đó hàm số đồng biến trên đoạn 0 ; 3
Khi đó M ax 0 ; 3 y = y 3 = 9 + 3 m 2 − 2 m 2 + 2 m − 9 = m 2 + 2 m ≤ 3 ⇔ − 3 ≤ m ≤ 1