Cho hàm số y = a x 4 + b x 2 + c ( a ≠ 0 ) có bảng biến thiên dưới đây:
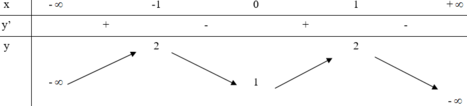
Tính P=a-2b+3c
A. P = 3.
B. P = 6.
C. P = -2.
D. P = 2.
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Đáp án A
Ta có: Đồ thị đi qua điểm (0,c) suy ra c = − 3
Tại x = 1 ⇒ y = a + b + c = − 5 ⇒ a + b = − 2
Do x = 1 là điểm cực trị suy ra y ' 1 = 0 ⇔ 4 a + 2 b = 0
Do đó c = − 3 a = 2 b = − 4 ⇒ P = − 15

a: Tọa độ đỉnh là:
\(\left\{{}\begin{matrix}x=\dfrac{-10}{2\cdot\left(-3\right)}=\dfrac{10}{6}=\dfrac{5}{3}\\y=-\dfrac{10^2-4\cdot\left(-3\right)\cdot\left(-4\right)}{4\cdot\left(-3\right)}=\dfrac{13}{3}\end{matrix}\right.\)
Bảng biến thiên:
| x | -\(\infty\) 5/3 +\(\infty\) |
| y | +\(\infty\) 13/3 -\(\infty\) |

b: Hàm số đồng biến khi x<5/3; nghịch biến khi x>5/3
Giá trị nhỏ nhất là y=13/3 khi x=5/3
Chọn C.
Phương pháp:
Dựa vào BBT để xác định các điểm mà đồ thị hàm số đi qua và các điểm cực trị của hàm số rồi từ đó xác định các giá trị a, b, c.
Cách giải:
Ta có:
Dựa vào bảng biến thiên, ta thầy đồ thị hàm số đi qua các điểm (-1; 2), (0; 1), (1; 2) và các các điểm này là các điểm cực trị của hàm số