Cho hai đoạn thẳng chéo nhau AB và CD. Gọi I và J lần lượt là trung điểm của AB và CD. Mệnh đề nào sau đây là đúng?
A. AC+BD>2IJ
B. AC+BD<2IJ
C. AC+BD>4IJ
D. AC+BD<4IJ
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

sao hả bạn bạn biết thì trả lời giúp mình còn ko thì đừng hỏi vớ vẩn nhé

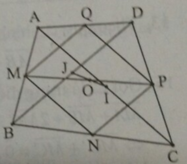
*Xét tam giác ABC có M; N là trung điểm của AB, BC nên MN là đường trung bình của tam giác.
⇒ M N / / A C ; M N = 1 2 A C ( 1 )
* Xét tam giác ADC có P; Q là trung điểm của CD, DA nên PQ là đường trung bình của tam giác.
⇒ P Q / / A C ; P Q = 1 2 A C ( 2 )
* Từ (1) (2) suy ra PQ// MN; PQ = MN. Do đó, tứ giác MNPQ là hình bình hành.
* Mà O là giao điểm của hình bình hành MNPQ nên O là trung điểm MP
* Xét tam giác ABC có MI là đường trung bình nên: M I / / B C ; M I = 1 2 B C ( 3 )
* Xét tam giác BCD có PJ là đường trung bình của các tam giác nên: P J / / B C ; P J = 1 2 B C ( 4 )
Từ (3) ( 4) suy ra ; tứ giác MIPJ là hình bình hành. Mà O là trung điểm MP nên điểm O là trung điểm của đoạn thẳng IJ. Từ đó ta có O I → = - O J →
Đáp án D

Bổ đề: Cho tứ giác lồi bất kì thì tổng hai cạnh đối bé hơn tổng hai đường chéo (dễ chứng minh bằng cách sử dụng bất đẳng thức tam giác) (**)
Gọi E là giao điểm của AB và CD. Có thể xảy ra hai khả năng: ^B ≥ ^C hoặc ^B ≤ ^C
Giả sử ^B ≥ ^C (không mất tính tổng quát)
Trên tia đối của tia JA lấy K sao cho JA = JK
Dễ dàng có AD = BK (tứ giác ABKD có hai đường chéo cắt nhau tại trung điểm của mỗi đường nên là hình bình hành)
IJ là đường trung bình của ∆ACK nên CK = 2IJ
Áp dụng bổ đề (**) vào tứ giác BCKD, ta được: BD + CK < CD + BK
Vậy BD + 2IJ < CD + AD (1)
Trong ∆ABC thì AC < AB + BC (2)
Cộng vế với vế (1) và (2), ta được: AC + BD + 2IJ < AB + BC + CD + DA
Gọi E là điểm đối xứng của A qua J, suy ra AC = DE.
Khi đó AC+BD = DE+BD > BE hơn nữa BE=2IJ (do IJ là đường trung bình của tam giác ABE)
Vậy AC+BC > 2IJ