Cho hàm số f ( x ) = x 4 - 4 x 3 + 2 x 2 - x + 1 ,∀ x∈ R. Tính ∫ 0 1 f 2 ( x ) . f ' ( x ) dx .
A. 2 3
B. 2.
C. - 2 3
D. -2
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
CM
Cao Minh Tâm
29 tháng 10 2018
Đúng(0)
Những câu hỏi liên quan
NV
Nguyễn Việt Lâm
Giáo viên
7 tháng 11 2021
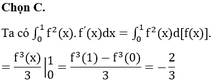
Vẫn là đạo hàm của tích
Dễ dàng viết được:
\(\left[f'\left(x\right)\right]^2+f\left(x\right).f''\left(x\right)=\left[f\left(x\right)\right]'.f'\left(x\right)+f\left(x\right).\left[f'\left(x\right)\right]'=\left[f'\left(x\right).f\left(x\right)\right]'\)
Do đó giả thiết biến đổi thành:
\(\left[f'\left(x\right).f\left(x\right)\right]'=15x^4+12x\)
Nguyên hàm 2 vế:
\(f'\left(x\right).f\left(x\right)=\int\left(15x^4+12x\right)dx=3x^5+6x^2+C\)
Thay \(x=0\)
\(\Rightarrow f'\left(0\right).f\left(0\right)=C\Rightarrow C=1\)
\(\Rightarrow f'\left(x\right).f\left(x\right)=3x^5+6x^2+1\)
Tiếp tục nguyên hàm 2 vế:
\(\int f\left(x\right).f'\left(x\right)dx=\int\left(3x^5+6x^2+1\right)dx\) với chú ý \(\int f\left(x\right).f'\left(x\right)dx=\int f\left(x\right).d\left[f\left(x\right)\right]=\dfrac{1}{2}f^2\left(x\right)+C\)
Nên:
\(\Rightarrow\dfrac{1}{2}f^2\left(x\right)=\dfrac{1}{2}x^6+2x^3+x+C\)
Thay \(x=0\Rightarrow C=\dfrac{1}{2}\)
\(\Rightarrow\dfrac{1}{2}f^2\left(x\right)=\dfrac{1}{2}x^6+2x^3+x+\dfrac{1}{2}\)
\(\Rightarrow f^2\left(1\right)\)
CM
24 tháng 7 2018
1 ) f ( x ) = 1 3 + 2 x + 1 3 + 2 x = 1 3 + 2 x + 2 x 3 . 2 x + 1 = 4 x + 6 . 2 x + 1 3 . 4 x + 10 . 2 x + 3
⇒ f ' ( x ) = 2 . 4 x . ln 2 + 5 . 2 x . ln 2 3 . 4 x + 10 . 2 x + 3 3 . 4 x + 10 . 2 x + 3 2
- 6 . 4 x . ln 2 + 10 . 2 x . ln 2 4 x + 6 . 2 x + 1 3 . 4 x + 10 . 2 x + 3 2
= 2 . 2 x + 6 3 . 4 x + 10 . 2 x + 3 - 6 . 2 x + 10 4 x + 6 . 2 x + 1 3 . 4 x + 10 . 2 x + 3 2 . 2 x . ln 2 = - 8 . 4 x + 8 3 . 4 x + 10 . 2 x + 3 2 . 2 x . ln 2
f ' ( x ) = 0 ⇔ - 8 . 4 x + 8 = 0 ⇔ 4 x = 1 ⇔ x = 0
2 ) f ( x ) = 4 x + 6 . 2 x + 1 3 . 4 x + 10 . 2 x + 3
Ta có
f ( x ) - 1 3 = 4 x + 6 . 2 x + 1 3 . 4 x + 10 . 2 x + 3 - 1 = - 2 . 4 x - 4 . 2 x - 2 3 . 4 x + 10 . 2 x + 3 < 0 , ∀ x ⇒ f ( 1 ) + f ( 2 ) + . . + f ( 2017 ) < 1 + 1 + . . . + 1 = 2017 ⇒ f ( 1 ) + f ( 2 ) + . . + f ( 2017 = 2017 ⇒ 2 ) s a i
3) f ( x 2 ) = 1 3 + 2 x + 1 3 + 2 - x ⇒ f ( x 2 ) = 1 3 + 4 x + 1 3 + 4 - x l à s a i
Chọn đáp án A.
10 tháng 5 2023
1: \(f'\left(x\right)=\dfrac{1}{3}\cdot3x^2+2x-\left(m+1\right)=x^2+2x-m-1\)
\(\Delta=2^2-4\left(-m-1\right)=4m+8\)
Để f'(x)>=0 với mọi x thì 4m+8<=0 và 1>0
=>m<=-2
=>\(m\in\left\{-10;-9;...;-2\right\}\)
=>Có 9 số
NV
Nguyễn Việt Lâm
Giáo viên
11 tháng 5 2021
Bài này chỉ có thể trắc nghiệm (dựa vào kết quả trắc nghiệm để suy luận) chứ không thể giải tự luận
Vì với mỗi hàm \(f\left(x\right)\) khác nhau sẽ cho những khoảng đồng biến - nghịch biến của \(g\left(x\right)\) khác nhau
NV
Nguyễn Việt Lâm
Giáo viên
4 tháng 4 2021
1a.
\(y'=3x^2.f'\left(x^3\right)-2x.g'\left(x^2\right)\)
b.
\(y'=\dfrac{3f^2\left(x\right).f'\left(x\right)+3g^2\left(x\right).g'\left(x\right)}{2\sqrt{f^3\left(x\right)+g^3\left(x\right)}}\)
2.
\(f'\left(x\right)=\left(m-1\right)x^3+\left(m-2\right)x^2-2mx+3=0\)
Để ý rằng tổng hệ số của vế trái bằng 1 nên pt luôn có nghiệm \(x=1\), sử dụng lược đồ Hooc-ne ta phân tích được:
\(\Leftrightarrow\left(x-1\right)\left[\left(m-1\right)x^2+\left(2m-3\right)x-3\right]=0\)
\(\Leftrightarrow\left[{}\begin{matrix}x=1\\\left(m-1\right)x^2+\left(2m-3\right)x-3=0\left(1\right)\end{matrix}\right.\)
Xét (1), với \(m=1\Rightarrow x=-3\)
- Với \(m\ne1\Rightarrow\Delta=\left(2m-3\right)^2+12\left(m-1\right)=4m^2-3\)
Nếu \(\left|m\right|< \dfrac{\sqrt{3}}{2}\Rightarrow\) (1) vô nghiệm \(\Rightarrow f'\left(x\right)=0\) có đúng 1 nghiệm
Nếu \(\left|m\right|>\dfrac{\sqrt{3}}{2}\Rightarrow\left(1\right)\) có 2 nghiệm \(\Rightarrow f'\left(x\right)=0\) có 3 nghiệm
