Giả sử z 1

PT

Pham Trong Bach

10 tháng 10 2019

Giả sử z 1 ; z 2 là các số phức khác 0 thỏa mãn điều kiện z 1 2 + z 2 2 = z 1 z 1 . Gọi A, B lần lượt là các điểm biểu diễn các số phức z 1 v à 2 z 2 - z 1 . Chọn mệnh đề đúng trong các mệnh đề sau: A. DOAB có một góc bằng 45 độ B. DOAB có một góc bằng 150...

Đọc tiếp

#Mẫu giáo

1

CM

Cao Minh Tâm

10 tháng 10 2019

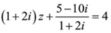
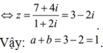
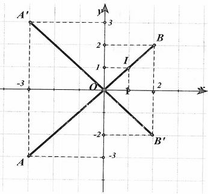
Chọn đáp án C.

Đúng(0)

PT

Pham Trong Bach

26 tháng 7 2019

Giả sử z=a+bi (a,b ∈ ℝ ) là số phức thỏa mãn (1+2i)z + 5 - 10 i 1 + 2 i =4. Tính tổng S=a+b ...

Đọc tiếp

#Toán lớp 12

1

CM

Cao Minh Tâm

26 tháng 7 2019

ĐÁP ÁN: B

Đúng(0)

PT

Phạm Thị Hoài Thu

24 tháng 2 2020 - olm

Giả sử x,y,z là những số thực dương thỏa mãn : 1/x+1/y+1/z=2.

Chứng minh rằng

√(x+1)+√(y+1)+√(z+1)≤√[5(x+y+z)].

#Toán lớp 9

2

T

tth_new

25 tháng 2 2020

\(VT=\sqrt{\left(\sqrt{x+1}+\sqrt{y+1}+\sqrt{z+1}\right)^2}\)

\(\le\sqrt{3\left(x+y+z+3\right)}=\sqrt{\left[9-2\left(x+y+z\right)\right]+5\left(x+y+z\right)}\)

\(=\sqrt{\left[9-\left(x+y+z\right)\left(\frac{1}{x}+\frac{1}{y}+\frac{1}{z}\right)\right]+5\left(x+y+z\right)}\le\sqrt{5\left(x+y+z\right)}=VP\)

Đẳng thức xảy ra khi \(a=b=c=\frac{3}{2}\)

Đúng(0)

KT

Không Tên

25 tháng 2 2020

Theo giả thiết \(2=\frac{1}{x}+\frac{1}{y}+\frac{1}{z}\ge\frac{9}{x+y+z}\Rightarrow x+y+z\ge\frac{9}{2}\)

\(\Rightarrow\frac{2}{3}\left(x+y+z\right)\ge3\)

\(VT=\sqrt{\left(\Sigma_{cyc}\frac{\sqrt{x+1}}{\sqrt{5\left(x+y+z\right)}}.\sqrt{5\left(x+y+z\right)}\right)^2}\le\sqrt{15\left(x+y+z\right)\left[\Sigma_{cyc}\frac{x+1}{5\left(x+y+z\right)}\right]}\)

\(=\sqrt{3\left(x+y+z+3\right)}\le\sqrt{3\left(x+y+z+\frac{2}{3}\left(x+y+z\right)\right)}=\sqrt{5\left(x+y+z\right)}=VP\)

Đúng(0)

BQ

Bùi Quang Sang

28 tháng 12 2018

Giả sử x.y.z = 1992

CMR : \(\dfrac{1992x}{xy+1992x+1992}+\dfrac{y}{zy+y+1992}+\dfrac{z}{xz+z+1}=1\)

#Toán lớp 8

1

NM

Nguyễn Minh Thịnh

3 tháng 1 2019

Ta có: \(\dfrac{1992x}{xy+1992x+1992}\)=

\(\dfrac{xyz.x}{xy+xyz.x+xyz}\) = \(\dfrac{xyz.x.z}{xy.z+xyz.x.z+xyz.z}\) = \(\dfrac{xz}{1+xz+z}\)

Ta có: \(\dfrac{y}{zy+y+1992}\)=\(\dfrac{y}{zy+y+xyz}\)=\(\dfrac{1}{z+1+xz}\)

=> \(\dfrac{1992x}{xy+1992x+1992}\)+\(\dfrac{y}{zy+y+1992}\)+\(\dfrac{z}{z+zx+1}\) = \(\dfrac{xz}{1+zx+z}\) +\(\dfrac{1}{z+zx+1}\) \(+\dfrac{z}{z+zx+1}\) =\(\dfrac{z+zx+1}{z+xz+1}\)

=1

Đúng(0)

PT

Pham Trong Bach

21 tháng 5 2019

Giả sử số phức z = − 1 + i − i 2 + i 3 − i 4 + i 5 − ... − i 99 + i 100 − i 101 . Lúc đó tổng phần thực và phần ảo của số phức z là A. 0 B. 1 C. i D....

Đọc tiếp

#Mẫu giáo

1

CM

Cao Minh Tâm

21 tháng 5 2019

Đáp án A

z = − 1 + i − i 2 + i 3 − i 4 + i 5 − ... + i 99 − i 100 + i 101 = − 1 + i + i 2 − 1 + i + i 4 − 1 + i + .... + i 100 − 1 + i = − 1 + i 1 + i 2 + i 4 + ... + i 100 = − 1 + i 1 1 − i 2.51 1 − i 2 = − 1 + i .

Đúng(0)

PT

Pham Trong Bach

18 tháng 5 2018

Cho số phức z thỏa z — + 3 i + 3 + z — - 2 i - 2 = 5 2 . Giả sử m, M lần lượt là giá trị nhỏ nhất và giá trị lớn nhất của z - i - 1 . Tinh S=M+m. A. S = 2 + 2 5 B. S = 4 2 C. S = 5 + 2 2 D. S = 2 ...

Đọc tiếp

#Mẫu giáo

1

CM

Cao Minh Tâm

18 tháng 5 2018

Đúng(0)

DT

Duy Tùng

20 tháng 4 2019

HELP giả sử z₁,z₂ là nghiệm pt ; Z²-2iZ-1-2i=0 khi đó z₁³+z₂³là

#Toán lớp 12

1

NV

Nguyễn Việt Lâm

Giáo viên

20 tháng 4 2019

Theo Viet: \(\left\{{}\begin{matrix}z_1+z_2=2i\\z_1z_2=-1-2i\end{matrix}\right.\)

\(\Rightarrow z_1^3+z_2^3=\left(z_1+z_2\right)\left(z_1^2+z_2^2-z_1z_2\right)=\left(z_1+z_2\right)\left(\left(z_1+z_2\right)^2-3z_1z_1\right)\)

\(=2i\left[\left(2i\right)^2-3\left(-1-2i\right)\right]=2i\left(6i-1\right)=-12-2i\)

Đúng(0)

PM

Phan Minh Anh

25 tháng 6 2021

Giả sử: a,b >0 và m,n ∈ Z*
Tìm min của: \(P=ax^m+b\dfrac{1}{x^n} \) với x>0

#Toán lớp 9

1

AH

Akai Haruma

Giáo viên

26 tháng 6 2021

Lời giải:

Áp dụng BĐT Cô - si:

\(P=ax^m+\frac{b}{x^n}=\frac{a}{n}x^m+\frac{a}{n}x^m+...+\frac{a}{n}x^m+\frac{b}{mx^n}+...+\frac{b}{mx^n}\)

\(=(m+n)\sqrt[m+n]{(\frac{a}{n})^n.x^{mn}.(\frac{b}{m})^m.\frac{1}{x^{mn}}}\)

\(=(m+n)\sqrt[m+n]{\frac{a^nb^m}{n^n.m^m}}\)

Đúng(0)

ND

Natsu Dragneel

25 tháng 12 2019

Giả sử x , y , z là những số dương thỏa mãn điều kiện x + y + z = 1 , tìm giá trị lớn nhất của

biểu thức P = \(\frac{x}{x+1}+\frac{y}{y+1}+\frac{z}{z+1}\)

#Toán lớp 9

1

HN

Ho Nhat Minh

27 tháng 12 2019

Ta co:

\(P=\Sigma_{cyc}\frac{x}{x+1}=3-\Sigma_{cyc}\frac{1}{x+1}\le3-\frac{9}{x+y+z+3}=\frac{9}{4}\)

Dau '=' xay ra khi \(x=y=z=\frac{1}{3}\)

Đúng(0)

PT

Pham Trong Bach

20 tháng 7 2019

Giả sử a, b là các số thực sao cho x 3 + y 3 = a .10 3 x + b .10 2 x đúng với mọi số thực dương x, y, z thỏa mãn log x + y = z và log x 2 + y 2 = z + 1. Giá trị của a+b bằng: A. − 31 2 . B. − 25 2 . C. 31 2 ...

Đọc tiếp

#Mẫu giáo

1

CM

Cao Minh Tâm

20 tháng 7 2019

Đáp án D.

Ta có:

log x + y = z log x 2 + y 2 = z + 1 ⇔ x + y = 10 z + x 2 + y 2 = 10 z + 1 = 10.10 z ⇒ x 2 + y 2 = 10 x + y

Khi đó:

x 3 + y 3 = a .10 3 z + b .10 2 z ⇔ x + y x 2 − x y + y 2 = a . 10 z 3 + b . 10 z 2 ⇔ x + y x 2 − x y + y 2 = a . x + y 3 + b . x + y 2 ⇔ x 2 − x y + y 2 = a . x + y 2 + b . x + y ⇔ x 2 − x y + y 2 = a . x 2 + 2 x y + y 2 + b 10 . x 2 + y 2 ⇔ x 2 + y 2 − x y = a + b 10 . x 2 + y 2 + 2 a . x y

Đồng nhất hệ số, ta được:

a + b 10 = 1 2 a = − 1 ⇒ a = − 1 2 b = 15 .

Vậy a + b = 29 2 .

Đúng(0)

Chúng tôi đề xuất

Tài nguyên

Ứng dụng mobile

Bảng xếp hạng

Các khóa học có thể bạn quan tâm

Yêu cầu VIP