Giúp mình với ạ chiều nay phải nộp rùi
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.



Hồn thơ chắt lọc từ cuộc đời long đong, côi cuốc, trưởng thành trong sự thiếu thốn tình cảm đối lập với hiện thực được sống trong danh gia vọng tộc. Đó chính là hồn thơ của Nguyễn Du, sớm mất cha lẫn mẹ, làm quan dưới hai triều đại Lê và Nguyễn. Ông đã sớm nhận ra cảnh lầm than, đói kém của thiên hạ, cảnh bất nhẫn của quan lại đối với nhân dân, tiếng nói của họ bị phớt lờ, quyền sống bị chà đạp đã nuôi dưỡng tâm hồn đại thi nhân thành con người có trái tim đôn hậu và thấm nhuần tư tưởng nhân đạo. Nguyễn Du đã đưa hai thể thơ của truyền thống dân tộc đạt đến trình độ điêu luyện và mẫu mực cổ điển. Đặt điểm nhìn thấu cảm từ tận đáy lòng mỗi nhân vật, từng con chữ vị hào kiệt viết ra là từng lời nói, từng nét vẽ hiện thực khắc nghiệt, chua xót về cuộc đời. Bên cạnh đó, ngôn ngữ thơ bậc tài đã đem đến những trang thơ rực rỡ, lẫy lừng hun đúc nên một hồn thơ đẹp, hồn thơ dân tộc, hồn thơ của đại nhân, hồn thơ Nguyễn Du

Bài 1:
\(a,A=6\sqrt{2}-6\sqrt{2}+2\sqrt{5}=2\sqrt{5}\\ b,B=\dfrac{\sqrt{3}\left(\sqrt{3}-1\right)}{\sqrt{3}-1}+\dfrac{\sqrt{2}\left(\sqrt{2}-1\right)}{\sqrt{2}-1}=\sqrt{3}+\sqrt{2}\\ c,=2\sqrt{3}-6\sqrt{3}+15\sqrt{3}-4\sqrt{3}=7\sqrt{3}\\ d,=1+6\sqrt{3}-\sqrt{3}-1=5\sqrt{3}\\ e,=4\sqrt{2}+\sqrt{2}-6\sqrt{2}+3\sqrt{2}=2\sqrt{2}\)
Bài 2:
\(a,ĐK:x\ge\dfrac{3}{2}\\ PT\Leftrightarrow\sqrt{2x-3}=5\Leftrightarrow2x-3=25\Leftrightarrow x=14\\ b,PT\Leftrightarrow x^2=\sqrt{\dfrac{98}{2}}=\sqrt{49}=7\Leftrightarrow\left[{}\begin{matrix}x=\sqrt{7}\\x=-\sqrt{7}\end{matrix}\right.\\ c,ĐK:x\ge3\\ PT\Leftrightarrow\sqrt{x-3}\left(\sqrt{x+3}+1\right)=0\\ \Leftrightarrow\sqrt{x-3}=0\left(\sqrt{x+3}+1>0\right)\\ \Leftrightarrow x=3\\ d,ĐK:x\ge1\\ PT\Leftrightarrow2\sqrt{x-1}-\sqrt{x-1}+3\sqrt{x-1}=4\\ \Leftrightarrow\sqrt{x-1}=1\Leftrightarrow x=2\left(tm\right)\\ e,PT\Leftrightarrow2x-1=16\Leftrightarrow x=\dfrac{17}{2}\\ f,PT\Leftrightarrow\left|2x-1\right|=\sqrt{3}-1\Leftrightarrow\left[{}\begin{matrix}2x-1=\sqrt{3}-1\\2x-1=1-\sqrt{3}\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}x=\dfrac{\sqrt{3}}{2}\\x=\dfrac{2-\sqrt{3}}{2}\end{matrix}\right.\)
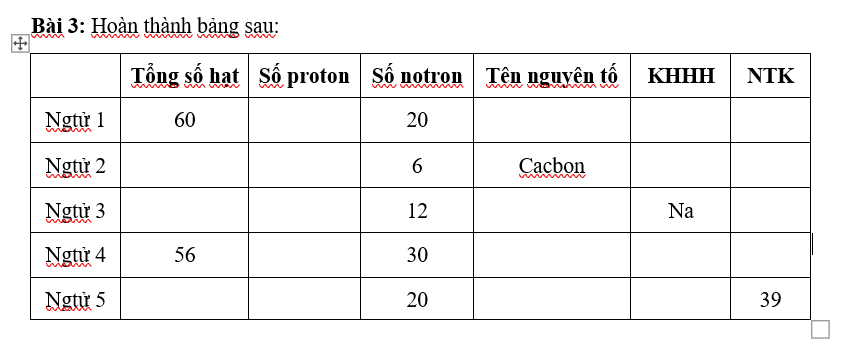
Bài 3:
\(a,Q=\dfrac{1+5}{3-1}=3\\ b,P=\dfrac{x+\sqrt{x}-6+x-2\sqrt{x}-3-x+4\sqrt{x}+9}{\left(\sqrt{x}-3\right)\left(\sqrt{x}+3\right)}\\ P=\dfrac{\sqrt{x}\left(\sqrt{x}+3\right)}{\left(\sqrt{x}-3\right)\left(\sqrt{x}+3\right)}=\dfrac{\sqrt{x}}{\sqrt{x}-3}\\ c,M=\dfrac{\sqrt{x}}{\sqrt{x}-3}\cdot\dfrac{3-\sqrt{x}}{\sqrt{x}+5}=\dfrac{-\sqrt{x}}{\sqrt{x}+5}\)
Vì \(-\sqrt{x}\le0;\sqrt{x}+5>0\) nên \(M< 0\)
Do đó \(\left|M\right|>\dfrac{1}{2}\Leftrightarrow M< -\dfrac{1}{2}\Leftrightarrow-\dfrac{\sqrt{x}}{\sqrt{x}+5}+\dfrac{1}{2}< 0\)
\(\Leftrightarrow\dfrac{2\sqrt{x}-\sqrt{x}-5}{2\left(\sqrt{x}+5\right)}< 0\Leftrightarrow\sqrt{x}-5< 0\left(\sqrt{x}+5>0\right)\\ \Leftrightarrow0\le x< 25\)
Bài 4:
\(a,A=\dfrac{16+2\cdot4+5}{4-3}=29\\ b,B=\dfrac{2\sqrt{x}-9-x+9+2x-3\sqrt{x}-2}{\left(\sqrt{x}-2\right)\left(\sqrt{x}-3\right)}\\ B=\dfrac{x-\sqrt{x}-2}{\left(\sqrt{x}-2\right)\left(\sqrt{x}-3\right)}=\dfrac{\left(\sqrt{x}-2\right)\left(\sqrt{x}+1\right)}{\left(\sqrt{x}-2\right)\left(\sqrt{x}-3\right)}=\dfrac{\sqrt{x}+1}{\sqrt{x}-3}\\ c,P=\dfrac{x+2\sqrt{x}+5}{\sqrt{x}-3}\cdot\dfrac{\sqrt{x}-3}{\sqrt{x}+1}=\dfrac{x+2\sqrt{x}+5}{\sqrt{x}+1}\\ P=\dfrac{\left(\sqrt{x}+1\right)^2+4}{\sqrt{x}+1}=\sqrt{x}+1+\dfrac{4}{\sqrt{x}+1}\\ P\ge2\sqrt{\left(\sqrt{x}+1\right)\cdot\dfrac{4}{\sqrt{x}+1}}=2\sqrt{4}=4\\ P_{min}=4\Leftrightarrow\left(\sqrt{x}+1\right)^2=4\Leftrightarrow\sqrt{x}+1=2\Leftrightarrow x=1\left(tm\right)\)

\(M=\frac{\left(101+1\right)101}{2}:\left[\left(101-100\right)+.....+\left(3-2\right)+1\right]\)
\(\Rightarrow M=\frac{102.101}{2}:\left(1+1+...+1\right)\)
\(\Rightarrow M=\frac{102.101}{2}:51\)
\(\Rightarrow M=\frac{51.2.101}{51.2}\)
\(\Rightarrow M=101\)
\(M=\left(101+100+.....+2+1\right):\left(101-100+.........-2+1\right)\)
\(M=\frac{\left(101+1\right).101}{2}:\left\{\left(101-100\right)+.......+\left(3-2\right)+1\right\}\)
\(M=5151:\left\{1+1+......+1+1\right\}\)
\(M=5151:51\\ M=101\)

Vật chuyển động thẳng đều:
Độ lớn lực kéo:
\(F_k=F_{ms}+m\cdot g=\mu mg+m\cdot g=0,4\cdot2\cdot10+2\cdot10=28N\)
Vật chuyển động với gia tốc 1m/s2 là:
Độ lớn lực kéo:
\(F_k=F_{ms}+m\cdot a=\mu mg+m\cdot a=0,4\cdot2\cdot10+2\cdot1=10N\)
a. Vật chuyển động thẳng đèu nên \(N=P=mg\)
Ta có: \(F_k=F_{ms}=\mu mg=0,4\cdot2\cdot10=8\left(N\right)\)
b. Áp dụng ĐL II Newton: \(\overrightarrow{F}+\overrightarrow{P}+\overrightarrow{N}+\overrightarrow{F_{ms}}=m\overrightarrow{a}\)
Chọn chiều dương là chiều chuyển động của xe, chiếu ptrinh lên chiều dương:
\(-F_{ms}+F_k=ma\)
\(F_k=\mu mg+ma=8+\left(2\cdot1\right)=10\left(N\right)\)

A)Theo đề bài:Phân tử A gồm X và 2H
X+2H=34
X+2.1=34
X+2=34
X=34-2=32(đvC)
X:sulfur(S)
Theo đề bài:Phân tử B gồm Y và 2O
Y+2O=46
Y+2.16=46
Y+32=46
Y=46-32=14(đvC)
Y:nitrogen(N)
B)X=32.100%=32%
Y=14.100%=14%
Có gì sai mong bạn bỏ qua (tại mik thấy bạn đang gấp nên mún giúp bạn 1 chút thuiiiii)chúc bạn đc điểm cao nhé

Bài 5:
a, Áp dụng PTG: \(BC=\sqrt{AB^2+AC^2}=5\left(cm\right)\)
\(\sin B=\dfrac{AC}{BC}=\dfrac{3}{5}\approx\sin37^0\\ \Rightarrow\widehat{B}\approx37^0\\ \Rightarrow\widehat{C}\approx90^0-37^0=53^0\)
b, Áp dụng HTL: \(S_{AHC}=\dfrac{1}{2}AH\cdot HC=\dfrac{1}{2}\cdot\dfrac{AB\cdot AC}{BC}\cdot\dfrac{AC^2}{BC}=\dfrac{1}{2}\cdot\dfrac{12}{5}\cdot\dfrac{9}{5}=\dfrac{54}{25}\left(cm^2\right)\)
c, Vì AD là p/g nên \(\dfrac{DH}{DB}=\dfrac{AH}{AB}\)
Mà \(AC^2=CH\cdot BC\Leftrightarrow\dfrac{HC}{AC}=\dfrac{AC}{BC}\)
Mà \(AH\cdot BC=AB\cdot AC\Leftrightarrow\dfrac{AH}{AB}=\dfrac{AC}{BC}\)
Vậy \(\dfrac{DH}{DB}=\dfrac{HC}{AC}\)

| Tổng số hạt | Số proton | Số notron | Tên nguyên tố | KHHH | NTK | |
| Nguyên tử 1 | 60 | 20 | 20 | Canxi | Ca | 40 |
| Nguyên tử 2 | 18 | 6 | 6 | Cacbon | C | 12 |
| Nguyên tử 3 | 36 | 12 | 12 | Magie | Mg | 24 |
| Nguyên tử 4 | Anh nghi 82 mới đúng | 26 | 30 | Sắt | Fe | 56 |
| Nguyên tử 5 | 58 | 19 | 20 | Kali | K | 39 |






A. Trắc nghiệm: 1.A; 2.B; 3.D; 4.D; 5.B; 6.C; 7.B; 8.C
B. Tự luận
Bài 4:
a/ Ta có AB//CD; \(AM\in AB;CN\in CD\) => AM//CN
AN//CM (gt)
=> AMCN là hbh (Tứ giác có các cặp cạnh đối // với nhau từng đôi 1 là hbh)
b/ Ta có
AD//CD; \(CI\in BC\) => AD//CI
AD=BC mà BC=CI => AD=CI
=> ACID là hbh (Tứ giác có cặp cạnh đối // và bằng nhau là hbh) => AC=DI (trong hbh các cặp cạnh đối = nhau từng đôi 1)
c/
Ta có
AM=BM (gt) \(\Rightarrow AM=\frac{AB}{2}\) mà AB=CD \(\Rightarrow AM=\frac{CD}{2}\)
Mà AMCN là hbh => AM=CN => \(CN=\frac{CD}{2}\) => N là trung điểm của CD (1)
AMCN là hbh => OA=OC (trong hbh 2 đường chéo cắt nhau tại trung điểm mỗi đường) => O là trung điểm của AC (2)
Từ (1) và (2) => NO là đường trung binhd của tg ACD (đường thẳng đi qua trung điểm của 2 cạnh một tam giác là đường trung bình)
d/ Trong hbh ACID nối AI cắt CD tại N' => N' là trung điểm của CD (trong hbh 2 đường chéo cắt nhau tại trung điểm mỗi đường)
Mà N là trung điểm của CD (cmt)
=> N trùng N'
Ta có
AMCN là hbh => MC//AN (Trong hbh các cặp cạnh đối // với nhau từng đôi 1)
Mà \(NI\in AN\)
=> MC//NI
Bài 5
\(A=-\left(y^4-8y^2+16\right)+20=-\left(y^2-4\right)^2+20\)
Ta có \(\left(y^2-4\right)\ge0\Rightarrow-\left(y^2-4\right)^2\le0\)
\(\Rightarrow A=-\left(y^2-4\right)+20\le20\)
Vậy giá trị lớn nhất của A là 20
Bài 5 (tiếp)
\(-\left(y^2-4\right)+20=20\Rightarrow y^2-4=0\Rightarrow y^2=4\Rightarrow y=\pm2\)