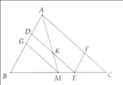
cho tam giác ABC đường trung tuyến AM điểm D thuộc cạnh AC gọi I là gđ của AM và BDqua C kẻ đường thẳng song song với AB cắt BD ở .CM hệ thức IB^2=ID.IK
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
10 tháng 3 2018
P/s hình tự vẽ lấy :)
Ta có: AM cắt CK tại E
Xét tam giác AMB và tam giác EMC có:
\(MB=MC\left(gt\right)\)
\(\widehat{AMB}=\widehat{CME}\)( đối đỉnh )
\(\widehat{ABM}=\widehat{ECM}\)( so le trong và AB // CE )
\(\Rightarrow\Delta AMB=\Delta EMC\left(g-c-g\right)\)
\(\Rightarrow MA=ME\)( hai cạnh tương ứng )
Và BM = MC ( Vì M là trung tuyến AM )
Suy ra ABCE là hình bình hành
\(\Rightarrow BE//AC\Rightarrow\frac{IB}{ID}=\frac{IA}{IE}\left(1\right)\)
\(\Rightarrow\frac{IB}{IK}=\frac{IA}{IE}\left(2\right)\)
Từ ( 1 ) và ( 2 ) suy ra \(\frac{ID}{IB}=\frac{IB}{IK}\)
\(\Rightarrow IB^2=ID.IK\left(đpcm\right)\)
Vậy \(IB^2=ID.IK\)
21 tháng 6 2022
Câu 3:
Xét ΔMDC có AB//CD
nên MA/MD=MB/MC(1)
Xét ΔMDK có AI//DK
nên AI/DK=MA/MD(2)
Xét ΔMKC có IB//KC
nên IB/KC=MB/MC(3)
Từ (1), (2) và (3) suy ra AI/DK=IB/KC=MI/MK
Vì AI//KC nên AI/KC=NI/NK=NA/NC
Vì IB//DK nên IB/DK=NI/NK
=>AI/KC=IB/DK
mà AI/DK=IB/KC
nên \(\dfrac{AI}{KC}\cdot\dfrac{AI}{DK}=\dfrac{IB}{DK}\cdot\dfrac{IB}{DC}\)
=>AI=IB
=>I là trung điểm của AB
AI/DK=BI/KC
mà AI=BI
nên DK=KC
hay K là trung điểm của CD
