Chứng minh các bất đẳng thức sau ( n ∈ N ∗ ) sin 2 n α + cos 2 n α ≤ 1 .
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
CM
Cao Minh Tâm
29 tháng 3 2019
Đúng(0)
Những câu hỏi liên quan
2 tháng 9 2018
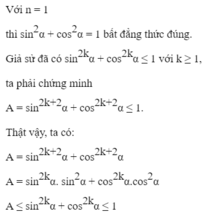
bài 1: ta có : \(cos^220+cos^240+cos^250+cos^270\)
\(=cos^220+cos^270+cos^240+cos^250\)
\(=cos^220+cos^2\left(90-20\right)+cos^240+cos^2\left(90-40\right)\)
\(=cos^220+sin^220+cos^240+sin^240=1+1=2\)
bài 2: a) ta có : \(cot^2\alpha-cos^2\alpha=cos^2\alpha\left(\dfrac{1}{sin^2\alpha}-1\right)=cos^2\alpha.\left(\dfrac{1-sin^2\alpha}{sin^2\alpha}\right)\)
\(=cos^2\alpha.\left(\dfrac{cos^2\alpha}{sin^2\alpha}\right)=cos^2\alpha.cot^2\alpha\left(đpcm\right)\)
b) ta có : \(sin^2\alpha+cos^2\alpha=1\Leftrightarrow sin^2\alpha=1-cos^2\alpha\)
\(\Leftrightarrow sin^2\alpha=\left(1-cos\alpha\right)\left(1+cos\alpha\right)\Leftrightarrow\dfrac{1+cos\alpha}{sin\alpha}=\dfrac{sin\alpha}{1-cos\alpha}\left(đpcm\right)\)
2 tháng 10 2021
a: \(\dfrac{\cos\alpha}{1-\sin\alpha}=\dfrac{1+\sin\alpha}{\cos\alpha}\)
\(\Leftrightarrow\cos^2\alpha=1-\sin^2\alpha\)(đúng)
2 tháng 10 2021
b: Ta có: \(\dfrac{\left(\sin\alpha+\cos\alpha\right)^2-\left(\sin\alpha-\cos\alpha\right)^2}{\sin\alpha\cdot\cos\alpha}\)
\(=\dfrac{4\cdot\sin\alpha\cdot\cos\alpha}{\sin\alpha\cdot\cos\alpha}\)
=4
5 tháng 7 2023
a: VT=sin^2a(sin^2a+cos^2a)+cos^2a
=sin^2a+cos^2a
=1=VP
b: \(VT=\dfrac{sina+sina\cdot cosa+sina-sina\cdot cosa}{1-cos^2a}=\dfrac{2sina}{sin^2a}=\dfrac{2}{sina}=VP\)
c: \(VT=\dfrac{sin^2a+1+2cosa+cos^2a}{sina\left(1+cosa\right)}\)
\(=\dfrac{2\left(cosa+1\right)}{sina\left(1+cosa\right)}=\dfrac{2}{sina}=VP\)
3 tháng 8 2020
Ta có:
(sin α+cos α)^2
=sin^2α + 2sin α cos α + cos^2 α
=1+2sin α cos α
Nên A đúng
(sin α−cos α)^2
=sin^2 α−2sin α cos α+cos^2α
=(sin^2α+cos^2α)−2sin α cos α
=1−2sin α cos α
Nên B đúng
cos^4 α−sin^4 α
=(cos^2 α−sin^2 α)(cos^2 α+sin^2 α)
=(cos^2 α−sin^2 α).1
=cos^2 α−sin^2 α
Nên C đúng
cos^4 α+sin^4 α
=(sin^2 α+cos^2 α )^2−2sin^2 α cos^2 α
=1−2 sin^2 α cos^2 α.
Nên D sai chọn D
ko bít có đúng ko nx
3 tháng 8 2020
Bạn ơi! Toán từ lớp 10 trở lên bạn vào hoc 24 để gửi câu hỏi nhé!
Bài này câu D sai.
Bạn thay \(\alpha=\frac{\pi}{2}\) vào thử nhé!
5 tháng 7 2019
\(A=\left(\sin\alpha+\cos\alpha+\sin\alpha-\cos\alpha\right)^2-2\left(\sin\alpha+\cos\alpha\right)\left(\sin\alpha-\cos\alpha\right)\)
\(=4\sin^2\alpha-2\sin^2\alpha+2\cos^2\alpha=2\left(\sin^2\alpha+\cos^2\alpha\right)=2\)
\(B=\sin^4\alpha+\cos^4\alpha+2\sin^2\alpha.\cos^2\alpha\left(\sin^2\alpha+\cos^2\alpha\right)=\sin^4\alpha+\cos^4\alpha+2\sin^2\alpha.\cos^2\alpha\)
\(=\left(\sin^2\alpha+\cos^2\alpha\right)^2-1=0\)
\(C=3\left(\sin^4\alpha+\cos^4\alpha\right)-2\sin^2\alpha.\cos^2\alpha\left(\sin^2\alpha+\cos^2\alpha\right)=3\left(\sin^4\alpha+\cos^4\alpha\right)-2\sin^2\alpha.\cos^2\alpha\)
\(=3\left(\sin^2\alpha+\cos^2\alpha-\frac{1}{9}\right)^2-\frac{1}{9}=\frac{61}{27}\)
