Question

[Pham Trong Bach]

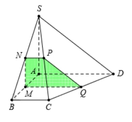
Hình chóp S.ABCD có đáy là hình thang vuông ABCD vuông tại A và D, có AB = 2a, AD = DC = a, có cạnh SA vuông góc với mặt phẳng (ABCD) và SA = a.

a) Chứng minh mặt phẳng (SAD) vuông góc với mặt phẳng (SDC), mặt phẳng (SAC) vuông góc với mặt phẳng (SCB).

b) Gọi φ là góc giữa hai mặt phẳng (SBC) và (ABCD), tính tanφ.

c) Gọi (α) là mặt phẳng chứa SD và vuông góc với mặt phẳng (SAC). Hãy xác định (α) và xác định thiết diện của hình chóp S.ABCD với (α)

Answer 1

[Cao Minh Tâm]

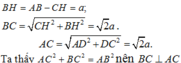
a) Ta có:

⇒ (SCD) ⊥ (SAD)

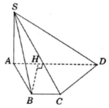
Gọi I là trung điểm của đoạn AB. Ta có AICD là hình vuông và IBCD là hình bình hành. Vì DI // CB và DI ⊥ CA nên AC ⊥ CB. Do đó CB ⊥ (SAC).

Vậy (SBC) ⊥ (SAC).

b) Ta có:

c)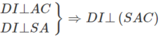 

Vậy (α) là mặt phẳng chứa SD và vuông góc với mặt phẳng (SAC) chính là mặt phẳng (SDI). Do đó thiết diện của (α) với hình chóp S.ABCD là tam giác đều SDI có chiều dài mỗi cạnh bằng a√2. Gọi H là tâm hình vuông AICD ta có SH ⊥ DI và  .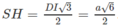

Tam giác SDI có diện tích: