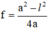Vật sang AB được đặt song song với màn và cách màn một khoảng cố định a.Một thất kính hội tụ có trục chính qua điểm A và vuông góc với màn được di chuyển giữa vật và màn. Đặt l là khoảng cách giữa hai vị trí trên của thấu kính. Hãy lập biểu thức của tiêu cự thấu kính f theo a và l. Suy ra một phương pháp đo tiêu cự của thấu kính hội tụ.
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
VT
17 tháng 12 2018
Sơ đồ tạo ảnh:
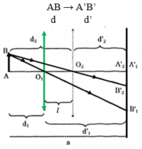
Ta có: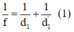 
Theo giả thiết: vật thật và ảnh trên màn ⇒ ảnh thật lớn hơn vật suy ra:
a = d1 + d’1 và d’1 > d1 > f > 0 (2)
Từ (1) và (2) ta có: d1.d’1 = f.(d1 + d’1) = f.a (3)
Theo định lý Vi-et đảo thì d1 và d’1 là nghiệm của phương trình: X2 – a.X + f.a = 0 (4)
Điều kiện để có hai vị trí của thấu kính cho ảnh rõ nét trên màn (E) là phương trình (4) phải có hai nghiệm X1 và X2.
Do đó ta phải có: Δ = a2 - 4fa ≥ 0 ⇒ f < a/4
Theo bất đẳng thức Cô-si:
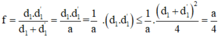
Vậy điều kiện Δ = a2 - 4fa ≥ 0 luôn đúng. Trường hợp Δ = 0 thì d1 = d’1 = a/2, khi đó 2 vị trí của thấu kính trùng nhau.
⇒ luôn tồn tại hai vị trí của thấu kính trong khoảng Vật-Màn đều cho ảnh rõ nét trên màn (ĐPCM)
H
14 tháng 6 2016
a) Chứng minh:
\(d+d' =a \Rightarrow d' = a -d\)
Và \(f=\frac{d.d'}{d+d'} \Rightarrow d = \frac{d.(a-d)}{a}\)
\( \Rightarrow d^2 -ad + af =0\)
\( \Delta = a^2 -4af =a(a-4f)\)
(Điều kiện để phương trình có nghiệm là \(a \geq 4f \))
Vì đã có 1 ảnh rõ nét rồi nên phương trình sẽ có nghiệm, vì có vị trí thứ 2 nữa nên phương trình phải có 2 nghiệm phân biệt.
Ta có hai vị trí này là 2 nghiệm có phương trình:
\( d_1 = \frac{a+ \sqrt{\Delta}}{2}\)
\(d_2 = \frac{a- \sqrt{\Delta}}{2}\)
b) Gọi l =khoảng cách 2 vị trí trên ta có:
\( l = d_2 -d_1 = \frac{a+ \sqrt { \Delta} - (a- \sqrt { \Delta})}{2} = \sqrt{\Delta} \)
Ta có: \(l^2 = \Delta = a^2 -4af \Rightarrow f = \frac{a^2 -l^2 }{4a}\)
Để đo tiêu cự chỉ cần đo khoảng cách giữa 2 vị trị cho ảnh rõ nét trên màn và khoảng cách giữa vật- màn. Phương pháp này gọi là phương pháp Bessel. Hoặc có thể dùng bất đẳng thức Cauchy để chứng minh cũng được nhé!
VT
21 tháng 12 2017
Đáp án cần chọn là: C
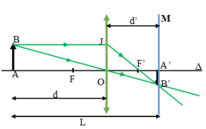
+ Khoảng cách vật và màn cố định, giữa vật và màn có hai vị trí thấu kính cho ảnh rõ nét trên màn thì theo nguyên lý về tính thuận nghịch của sự truyền ánh sáng, hai vị trí này phải có tính chất đối xứng, tức là:
d 1 ' = d 2 và d 2 ' = d 1 (1)
+ Theo giả thiết: k = A 1 B 1 A 2 B 2 = 4
+ Lại có: k = A 1 B 1 A 2 B 2 = A 1 B 1 ¯ A 2 B 2 ¯ = A 1 B 1 ¯ A B ¯ . A B ¯ A 2 B 2 ¯ = k 1 k 2 (2)
+ k 1 = − d 1 ' d 1 ; k 2 = − d 2 ' d 2 (3)
Từ (1); (2) và (3) ta có: k = d 1 ' d 1
→ k d 1 ' = 1 d 1
Theo tính chất phân thức: k d 1 ' = 1 d 1 = k + 1 L (*)
+ Theo công thức thấu kính: f = d 1 d 1 ' d 1 + d 1 ' = d 1 d 1 ' L (**)
Từ (*) và (**), ta được: f = L k k + 1 2
Thay số, được: f = 10 c m
VT
7 tháng 10 2017
Chọn đáp án A.
Ta có: f = d . d ' d + d ' (1)
Khoảng các giữa vật và màn đo được gấp 7,2 lần tiêu cự: d + d ' = 7 , 2 f (2) d + d ' = − 7 , 2 f (3)
Do ảnh là ảnh thật hiện được trên màn nên d > 0 , d ' > 0 nên chỉ xảy ra trường hợp (2).
Từ (1) và (2), được: f = d . d ' d + d ' = d + d ' 7 , 2 ⇔ 7 , 2 d d ' = d 2 + 2 d d ' + d ' 2
Chia cả hai vế có d 2 : 7 , 2 d ' d = 1 + 2. d ' d + d ' d 2
Hệ số phóng đại k = − d ' d , thay lên được: k 2 + 5 , 2 k + 1 = 0 ⇒ k = − 0 , 2 k = − 5
Dấu “-” chứng tỏ ảnh thật, ngược chiều với vật.
Mặt khác: k = h ' h ⇒ k = 0 , 2 ⇒ h ' = 0 , 2 h = 0 , 4 c m k = 5 ⇒ h ' = 5.2 = 10 c m
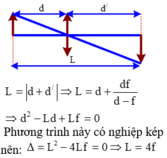
Theo đề: l = d2 - d1 = √Δ
Ta có: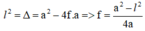
∗ Vậy muốn tìm tiêu cự của thấu kính ta dùng thí nghiệm để tìm được hai vị trí của thấu kính cho ảnh rõ trên màn. Sau đó:
- Đo khoảng cách vật – màn bằng a.
- Đo khoảng cách l giữa hai vị trí của thấu kính cho ảnh rõ nét trên màn.
- Áp dụng công thức: